Como se indicó en la sección 14.3, la programación separable supone que la función objetivo f(x) es cóncava, que cada una de las funciones de restricción gi(x) es convexa y que todas estas funciones son funciones separables (funciones en las que cada término incluye una sola variable). Sin embargo, con el fin de simplificar la presentación, la atención de esta sección se centra en el caso especial en el que las funciones gi(x) convexas y separables de hecho son funciones lineales, como las de programación lineal. Así, solo la función objetivo requerirá un tratamiento especial.
sábado, 26 de diciembre de 2015
Programación separable (I)
Como se indicó en la sección 14.3, la programación separable supone que la función objetivo f(x) es cóncava, que cada una de las funciones de restricción gi(x) es convexa y que todas estas funciones son funciones separables (funciones en las que cada término incluye una sola variable). Sin embargo, con el fin de simplificar la presentación, la atención de esta sección se centra en el caso especial en el que las funciones gi(x) convexas y separables de hecho son funciones lineales, como las de programación lineal. Así, solo la función objetivo requerirá un tratamiento especial.
viernes, 25 de diciembre de 2015
Método Símplex Modificado - Ejemplo (IV)
jueves, 24 de diciembre de 2015
Método Símplex Modificado - Ejemplo (III)
La tabla 14.4 muestra los resultados de la aplicación del método símplex modificado a este problema. La primera tabla símplex exhibe el sistema de ecuaciones inicial después de convertir de minimización de Z a maximización de (-Z) y de eliminar algebraicamente las variables básicas iniciales de la ecuación (0), lo mismo que se hizo para el ejemplo de terapia de radiación en la sección 4.6. Las tres iteraciones procedenigual que en el método simplex normal, excepto por la eliminación de ciertos candidatos para la variable básica entrante, según la regla de entrada restringida. En la primera tabla se elimina u1 como candidato porque su variable complementaria (v1) es ya una variable básica (de todas maneras, habría entrado x2 puesto que -4 < - 3). En la segunda tabla se elimina tanto u1 como y2 (puesto que v1 y x2 son variables básicas) y de manera automática se elige x1 como único candidato con coeficientes negativos en el renglón 0 (mientras que el método símplex normal habría permitido la entrada o bien de x1 o de u1, porque están empatadas con el coeficiente más negativo). En la tercera tabla se eliminan y1 y y2 (porque x1 y x2 son variables básicas). Esta vez u1 no se elimina, pues v1 ya no es una variable básica, así que se elige u1 como variable entrante.
miércoles, 23 de diciembre de 2015
Método Símplex Modificado - Ejemplo (II)
x1y1 + x2y2 + u1v1 = 0,
no se incluye explícitamente, porque el algoritmo refuerza esta restricción de manera automática con la regla de entrada restringida. En particular, para cadauno de los tres pares de variables complementarias [(x1, y1), (x2, y2), (u1, v1)], siempre que una de las dos variables sea ya una variable básica, la otra se excluye de los candidatos como variable básica entrante. Como el conjunto inicial de variables básicas para el problema de programación lineal [z1, z2, v1] da una solución básica factible inicial que satisface la restricción de complementariedad, no hay manera de violar esta restricción con ninguna de las restricciones básicas factibles subsecuentes.
martes, 22 de diciembre de 2015
Método Símplex Modificado - Ejemplo (I)
lunes, 21 de diciembre de 2015
Método Símplex Modificado - Regla de entrada restringida
Esta regla conserva satisfecha la restricción de complementariedad en todo el curso del algoritmo. Cuando se obtiene una solución óptima.
x*, u*, y*, v* z1 = 0,............................, zn = 0
para la fase I de este problema, x* es la solución óptima deseada para el problema original de programación cuadrática. La fase 2 del método de do fases no se necesita.
martes, 15 de diciembre de 2015
Método Símplex Modificado (III)
sujeta a las restricciones anteriores de programación lineal, obtenidas de las condiciones KKT, pero con estas variables artificiales incluidas.
La modificación al método símplex es el siguiente cambio en el procedimiento para elegir una variable básica entrante.
sábado, 7 de noviembre de 2015
Método Símplex Modificado (II)
viernes, 6 de noviembre de 2015
Método Símplex Modificado (I)
jueves, 5 de noviembre de 2015
Condiciones KKT para programación cuadrática (VI)
Como se supone que la función objetivo del problema original es cóncava y como las funciones de restricción son lineales y, por tanto, convexas, se puede aplicar el colorario del teorema de la sección 14.6. Así, x es óptima si y sólo si existen valores de y, y y v talse que los cuatro vectores juntos satisfagan todas estas condiciones. Así pues, el problema original se reduce al problema equivalente de encontrar una solución factible para estas restricciones.
Es interesante observar que este problema equivalente es un ejemplo del problema de complementariedad lineal introducido en la sección 14.3 (véase el problema 13), y que una restricción clave para este problema de complementariedad lineal es su restricción de complementariedad.
miércoles, 4 de noviembre de 2015
Condiciones KKT para programación cuadrática (V)
en donde los elementos del vector columna u son las ui de la sección anterior y lo elementos de los vectores columna y y v son variables de holgura.
martes, 3 de noviembre de 2015
Condiciones KKT para programación cuadrática (IV)
Esta forma e en espcial conveniente ya que excepto por la restricción de complementariedad, estas condiciones son restricciones de programación lineal.
lunes, 2 de noviembre de 2015
Condiciones KKT para programación cuadrática (III)
xiy1 + x2y2 + u1v1 = 0
llamada restricción de complementariedad
domingo, 1 de noviembre de 2015
Condiciones KKT para programación cuadrática (II)
sábado, 31 de octubre de 2015
Condiciones KKT para programación cuadrática (I)
viernes, 30 de octubre de 2015
Programación cuadrática (II)
jueves, 29 de octubre de 2015
Programación cuadrática (I)
miércoles, 28 de octubre de 2015
Ejemplo Teorema de Karush-Kuhn-Tucker (KKT) (IV)
En problemas más complicados que éste puede ser difícil, si no es materialmente imposible, derivar una solución óptima directa de las condiciones KKT. De todas maneras estas condiciones proporcionan información valiosa en cuanto a la identidad de una solución óptima y también permiten verificar que una solución propuesta sea óptima.
Existen mucha aplicaciones indirectas valiosas de las condiciones KKT. Una de ellas surge en la teoría de la dualidad desarrollada par programación no lineal, que se puede poner en parelelo con la teoría de la dualidad para programación líneal presentada en el capítulo 6. En particular, para cualquier problema de maximización restringida (llámese problema primal), se pueden usar las condiciones KKT para definir un problema dual asociado, que es un problema de minización restringido. Las variables del problema dual consisten en multiplicadores de Lagrange, ui = (i = 1,2,......, m) y las variables primales xj (j = 1,2....., n). En el caso especial de que el problema primal es un problema de programación lineal, las variables xj desaparecerán del problema dual y quedará el familiar problema dual de programación líneal (en el que las variables ui, aquí corresponden a las variables yi del capítulo 6). Cuando un problema primal es un problema de programación convexa, es posible establecer relaciones entre el problema primal y el problema dual, que son muy parecidas a las de programación lineal. Por ejemplo,la propiedad dualidad fuerte de la sección 6.1, que establece que los valore óptimos de las funciones objetivo son iguales, también se cumple aquí. Más aún, los valores de las variables ui en una solución óptima para el problema dual,de nuevo se pueden interpretar como los precios sombra (véanse las secciones 4.7 y 6.2); es decir, proporcionan la tasa a la que puede aumentar el valor óptimo de la función objetivo para el problema primal, si se aumenta (ligeramente) el lado derecho de la restricción correspondiente. Como la teoría de dualidad para programación no lineal es un tema relativamente avanzado se pide al lector interesado que consulte otros libros para obtener la información.
En la sección siguiente se verá otra aplicación indirecta de la condiciones KKT.
martes, 27 de octubre de 2015
lunes, 26 de octubre de 2015
Ejemplo Teorema de Karush-Kuhn-Tucker (KKT) (II)
domingo, 25 de octubre de 2015
Ejemplo Teorema de Karush-Kuhn-Tucker (KKT) (I)
sábado, 24 de octubre de 2015
Teorema de Karush-Kuhn-Tucker (KKT) (III) Corolario
viernes, 23 de octubre de 2015
Teorema de Karush-Kuhn-Tucker (KKT) (II)
jueves, 22 de octubre de 2015
miércoles, 21 de octubre de 2015
Condiciones de Karush-Kuhn-Tucker (KKT) para optimización restringida
En las secciones anteriores se hicieron notar estas condiciones para optimización no restringida, como se resume en los primeros dos renglones de la tabla 14.3. Al principio de la sección 14.3, también se expusieron estas condiciones para la ligera extensión de optimización no restringida cuando sólo se tienen restricciones de no negatividad. En la tabla 14.3 se muestran estas condiciones en el tercer reglón, en otra forma equivalente a la que sugiere la ampliación para optimización restringida general. Como se indica en el último renglón de la tabla, las condiciones para el caso general se llaman condiciones de Karush-Kuhn-Tucker (o condiciones KKT), porque fueron desarrolladas independientemente por Karush y por Kuhn y Tucker. Su resultado básico se expresa en el siguiente teorema.
martes, 20 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente - Ejemplo (V)
lunes, 19 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente - Ejemplo (IV)
La figura 14.11 sugiere que el procedimiento de búsqueda del gradiente marca una trayectoria en zigzag hacia la solución óptima en lugar de moverse en línea recta. Tomando en cuenta este comportamiento, se han realizado algunas modificaciones que aceleran el movimiento hacia el óptimo.
Si f(x) no fuera una función cóncava, este procedimiento convergiría en un máximo local.
El único cambio en la descripción del procedimiento para este caso es que t* ahora corresponde al primer máximo local de f(x'+ t▽f(x'), conforme t aumenta su valor.
domingo, 18 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente - Ejemplo (III)
sábado, 17 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente - Ejemplo (II)
viernes, 16 de octubre de 2015
jueves, 15 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente (II)
Regla de detención
se evalúa ▽f(x') en x = x'. Se verifica siSi es así, el proceso se detiene con la x'actual como la aproximación a una solución óptima x* deseada. De otra manera, se regresa al paso iterativo.
miércoles, 14 de octubre de 2015
Resumen del procedimiento de búsqueda del gradiente
martes, 13 de octubre de 2015
Procedimiento de búsqueda del gradiente (III)
lunes, 12 de octubre de 2015
Procedimiento de búsqueda del gradiente (II)
Una anología puede ayudar a aclarar este procedimiento. Supóngase que una persona quiere subir a la cumbre de una montaña. Esta persona es miope y no puede ver la cumbre para caminar en esa dirección, pero cuando se detiene, puede ver el piso a su alrededor y determinar la dirección en la que la pendiente de la montaña es más pronunciada. La persona puede caminar en línea recta. Mientras camina, también es capaz de percibir cuándo ya no va hacia arriba (pendiente cero en esa dirección). Suponiendo que la montaña es cóncava, el individuo puede usar el procedimiento de búsqueda del gradiente para escalar hasta la cima eficientemente. Este problema tiene dos variables, en donde (x1, x2) representa las coordenadas (ignorando la altura) de la localización actual. La función f(x1, x2) da la altura de la montaña en (x1, x2). La persona comienza cada iteración en su localización actual (solución prueba actual) al determinar la dirección [en el sistema de coordenadas (x1, x2)] en la que la montaña tiene la mayor pendiente (la dirección del gradiente) en este punto. Después, comienza a caminar en otra dirección fija y continúa haciéndolo mientras sigue subiendo. Luego se detiene en una nueva localización (solución) prueba, cuando la montaña se nivela en la dirección en que camina. Estas iteraciones continúan, siguiendo una trayectoria en zig-zag hacia arriba, hasta que e alcanza una localización prueba en la que la pendiente es esencialmente cero en todas direcciones. Bajo la suposición de que la montaña [f(x1, x2)] es cóncava, en principio, la persona debe estar en la cima de la montaña.
domingo, 11 de octubre de 2015
Procedimiento de búsqueda del gradiente (I)
sábado, 10 de octubre de 2015
Optimización no restringida de varias variables (III)
viernes, 9 de octubre de 2015
Optimización no restringida de varias variables (II)
En la sección 14.4 se usó el valor de la derivada ordinaria para elegir una de sólo dos direcciones posibles (aumentar x o disminuir x) para pasar de la solución prueba actual a la siguiente. La meta era alcanzar en algún momento un punto en el que la derivada fuera (esencialmente) cero. Ahora se tienen innumerables direcciones posibles hacia dónde moverse; corresponden a las tasas proporcionales posibles a las cuales las respectivas variables pueden cambiar. La meta es alcanzr eventualmente un punto en el qeu todas las derivadas parciales sean (en esencia) cero. Por tanto, la extensión del procedimiento de búsqueda en una dimensión requiere emplear los valores de las derivadas parciales para seleccionar la dirección específica en la que conviene moverse. Esta selección implica el uso del gradiente dela función objetivo, como se describirá en seguida.
jueves, 8 de octubre de 2015
Optimización no restringida de varias variables (I)
Ahora considerese el problema de maximizar una función cóncava f(x) de varias variables (o de variables múltiples), x = (x1, x2,......., xn) en la que no se tiene retricciones sobre los valores factibles. Supóngase de nuevo que la condición necesaria y suficiente para la optimalidad, dada por el sistema de ecuaciones que se obtiene al establecer las repectivas derivadas praciales iguales a cero, no e puede resolver análiticamente, por lo que debe emplearse un procedimiento de búsqueda númerico. Cómo puede extenderse el procedimiento de búsqueda en una dimensión a este problema multidimensional??.
miércoles, 7 de octubre de 2015
Procedimiento de búsqueda en una dimensión - Paso inicial Ejemplo (II)
Como la segunda derivada es no positiva en todos lados, f(x) es una función cóncava, y el procedimiento de búsqueda se aplica sin problemas para encontrar su máximo global. Una rápida inspección a esta función (sin construir siquiera la gráfica de la figura 14.10) indica que f(x)es positiva para valores pequeños de x, pero es negativa para x < 0 o x > 2. Entonces, x(barra abajo) = 0 y x(barra arriba) =2 se pueden usar como cotas iniciales, con su punto medio x' = 1, como solución prueba inicial. Sea 0.01 la tolerancia del error para x* en la regla de detención, de manera que (x(barra arriba) - x(barra abajo)) ≤ 0.02 con la x'final en el punto medio. Al aplicar el procedimiento de búsqueda en una dimensión se obtiene la sucesión de resultados que se muestranen la tabla 14.1 [Esta tabla incluye tanto los valores de la función como los de la derivada, para información del lector, en donde la derivada se evalúa en la solución prueba que se genera en la interación anterior. Obsérvese que, de hecho, el algoritmo no necesita calcular f(x') y que sólo tiene que calcular la derivada hasta el punto en que se pueda determinar su signo]. La conclusión es que
x* ≈ 0.836
0.828125 < x* < 0.84375
martes, 6 de octubre de 2015
lunes, 5 de octubre de 2015
Procedimiento de búsqueda en una dimensión - Paso inicial
domingo, 4 de octubre de 2015
Procedimiento de búsqueda en una dimensión (III)
Resume el procedimiento de búsqueda en una dimensión.
sábado, 3 de octubre de 2015
Procedimiento de búsqueda en una dimensión (II)
Por el contrario, si la derivada es negativa, entonces x* debe ser más chica que esta x, y x se convierte en una cota superior. Una vez que se han indentificado ambas cotas, cada nueva solución prueba que se selecciona entre ellas proporciona una nueva cota más estrecha de uno de los dos tipos, cerrando la búsqueda cada vez más. Siempre y cuando se usa una regla razonable para elegir cada solución prueba en esta forma, la sucesión de soluciones prueba debe converger a x*. En la práctica, esto significa continuar la sucesión, hasta que la distancia entre las cotas sean lo suficientemente pequeña como para que la siguiente solución prueba se encuentre dentro de una tolerancia de error de x* preespecificada.
En eguida se resume este proceso completo, usando la notación

viernes, 2 de octubre de 2015
Procedimiento de búsqueda en una dimensión (I)
jueves, 1 de octubre de 2015
Optimización no restringida de una variable (I)
df/dx = 0 en x = x*
como se bosqueja en la figura 14.9. Si en esta ecuación se puede despejar directamente x*, el problema llegó a su fin, pero si f(x) no e una función sencilla y su derivada no es una función lineal o cuadrática, tal vez sea imposible resolver la ecuación analíticamente. De ser así, el procedimiento de búsqueda en una dimensión proporcionauna forma directa de resolverlo númericamente.
miércoles, 30 de septiembre de 2015
Problema de complementariedad (III)
F(x) = q + Mz.
en donde q es un vector columna dado y M es una matriz p x p dada. Se dispone de algoritmos eficientes para resolver este problema bajo algunas suposiciones adecuadas sobre las propiedades de la matriz M. Uno de estos requiere pivotear de una solución básica factible a la siguiente, en forma muy parecida a la del método símplex para programación lineal.
Además de tener aplicaciones en programación no lineal, los problemas de complementariedad se utilizan en teoría de juegos, problemas de equilibrio económico y problemas de equilibrio en ingeniería.
martes, 29 de septiembre de 2015
Problema de complementariedad (II)
wi = 0 o zi = 0 (o ambas) para cada i = 1, 2, ....., p
lunes, 28 de septiembre de 2015
Problema de complementariedad (I)
w = F(z) w ≤ 0, z ≥ 0,
Que tambien satisface la restricción de complementariedad
w^Tz =0
domingo, 27 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación Fraccional (II)
que se puede resolver con el método símplex. En términos generales, se puede usar el mismo tipo de transformación para convertir un problema de programación fraccional con f1(x) cóncava, f2(x) convexa y gi(x) convexas, en un problema equivalente de programación convexa.
sábado, 26 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación Fraccional (I)
Maximizar f(x) = f1(x)/f2(x)
Estos problemas de programación fraccional surgen, por ejemplo, cuando se maximiza la razón de la producción entre la horas-hombre empleadas (productividad), o la ganancia entre el capital invertido (tasa de crecimiento), o el valor esperado entre la desviación estandar de alguna medida de desempeño para una cartera de inversiones (rendimiento/riesgo). Se han formulado algunos procedimientos de solución especiales para ciertas formas de f1(x) y f2(x).
viernes, 25 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación geométrica (II)
en todo el modelo orifinal, y se puede aplicar un algoritmo de programación convexa. Se cuenta con otro procedimiento de solución para resolver estos problemas de programación posinomial, al igual que para problemas de programación geométrica de otros tipos.
jueves, 24 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación geométrica (I)
miércoles, 23 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación no convexa
Ciertos tipso específicos de problemas de programación no convexa se pueden resolver sin mucha dificultad mediante métodos especiales. Dos de ellos, de gran importancia, se presentarán mmás adelante.
martes, 22 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación Separable
La programación separable es un caso especial de programación convexa, en donde la suposición adicional es
3. Todas la funciones f(x) y gi(x) son funciones separables.
Una función separable es una función en la que cada término incluye una sola variable, por lo que la función se puede separar en una suma de funciones de variables individuales. Por ejemplo, si f(x) es una función separable, se puede expresar como
en donde cada fj(xj) incluye sólo los términos con xj. En la terminología de programación lineal (véase la sección 3.3) , los problemas de programación separable satisfacen las suposiciones de aditividad pero no las de proporcionalidad (para funciones no lineales).
Es importante distinguir estos problemas de otros de programación convexa, ya que cualquier problema de programación separable se puede aproximar muy de cerca mediante uno de programación lineal y, entonces, se puede aplicar el eficiente método símplex. Este enfoque se describe en la sección 14.8 (Para simplificar, se centra la atención en el caso linealmente restringido, en el que el tratamiento especial se necesita nada más para la función objetivo.)
lunes, 21 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación Convexa
La programación convexa abarca una amplia clase de problemas entre los que se encuentran como casos especiales, todos los tipos anteriores cuando f(x) es cóncava. Las suposiciones son
1. f(x) es cóncava
2. Cada una de las gi(x) son convexas.
Como se dijo al final de la sección 14.2, estas suposiciones son suficientes para asegurar que un máximo local es un máximo global. En la sección 14.6 se verá que las condiciones y suficientes para obtener tal solución óptima son una generalización natural de las condiciones que se acaban de exponer para la optimización no restringida y su extensión a la inclusión de restricciones de no negatividad. La sección 14.9 describe los enfoques algorítmicos para resolver problemas de programación convexa.
domingo, 20 de septiembre de 2015
Tipos de problemas de programación no lineal - Programación Cuadrática
DE nuevo los problemas de programación cuadrática tienen restricciones lineales, pero ahora la función objetivo f(x) debe ser cuadrática. Entonces, la única diferencia entre éstos y un programa de programación lineal es que algunos términos de la función objetivo incluyen el cuadrado de una variable o el producto de dos variables.
Se han desarrollado muchos algoritmos para este caso, con la suposición adicional de que f(x) es cóncava. La sección 14.7 presenta un algoritmo que maneja una extensión del método símplex.
La programación cuadrática es muy importante, en parte porque las formulaciones de este tipo surgen de manera natural en muchas aplicaciones. Por ejemplo, el problema de la selección de una cartera con inversiones riesgosas, descrito en la sección 14.1 se ajusta a este formato. Sin embargo, otra razón por la que es importante es que al resolver problemas generales de optimización linealmente restringida se puede obtener la solución de una sucesión de aproximaciones de programación cuadrática.
sábado, 19 de septiembre de 2015
Tipos de problemas de programación no lineal - Optimización linealmente restringida
Los problemas de optimización linealmente restringida se caracterizan por restricciones que se ajustan completamente a la programación líneal, de manera que todas las funciones de restricción gi(x) son lineales, pero la función objetivo es no lineal. El problema se simplifica mucho si sólo se tien que tomar en cuenta una función no lineal y una región factible de programación lineal. Se han desarrollado varios algortimos especiales basados en una extensión del método símplex para analizar la función objetivo no lineal.
Un caso especial importante es la programación cuadrática.
viernes, 18 de septiembre de 2015
Tipos de problemas de programación no lineal - Optimización no restringida (II)
Cuando una vriable xj tiene una restricción de no negatividad, xj ≥ 0, la condición necesaria (y tal vez) suficiente anterior cambi ligeramente a:
jueves, 17 de septiembre de 2015
Tipos de problemas de programación no lineal - Optimización no restringida (I)
Maximizar f(x)
sobre todos los valores x = (x1, x2,.......xn). Según se repasa en el apéndice 2, la condición necesaria para que una solución específica x = x* sea óptima cuando f(x) es una función diferenciable es:
∂f/∂xj = 0 en x = x*, para j = 1,2,.....,n.
miércoles, 16 de septiembre de 2015
Tipos de problemas de programación no lineal
martes, 15 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (VI)
lunes, 14 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (V)
Las funciones de las variables múltiples también se pueden caracterizar como cóncavas o convexas si su curvatura es siempre hacia abajo o hacia arriba. Por ejemplo, considérese una función que consiste en una suma de términos. Si todos los términos son cóncavos (se puede verificar que lo sea, con su segunda derivada cuando el término incluye nada más una de las variables), entonces la función es cóncava. De manera similar, la función es convexa i todos los términos son convexos. Estas definiciones intuitivas se fundamentan en términos precisos que, junto con un poco de profundización en los conceptos, se presentanen el apéndice I.
domingo, 13 de septiembre de 2015
sábado, 12 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (IV)
d²f/dx² ≤ para toda x
viernes, 11 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (III)
Z = 54x1 - 9x1² + 78x2 - 13x2²
entonces la solución óptima resulta (x1, x2) = (3,3), que se encuentra dentro de la frontera de la región factible. (SE puede comprobar que esta solución es óptimasi se usa el Cálculo para derivarla como un máximo global no restringido; como también satisface las restricciones, debe ser óptima para el problema restringido). Por lo tanto, es necesario que un algoritmo general para resolver problemas de este tipo tome en cuenta toda las soluciones en la regiónn factible y no sólo aquéllas que están sobre la frontera.
Otra complicación que surge en la programación no líneal es que un máximo local no necesariamente es un máximo global (la solución óptima global). Por ejemplo, considérese la función de una sola variable graficada en la figura 14.7. En el intervalo 0 ≤ x ≤ 5, esta función tiene tres máximos locales, x = 0, x = 2, x = 4, pero sólo uno de estos, x = 4, e un máximo global. (De igual manera, existen mínimo locales en x = 1, 3 y 5, pero sólo x = 5 es un mínimo global)
jueves, 10 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (II)
miércoles, 9 de septiembre de 2015
Ilustración gráfica de problema de programación no lineal (I)
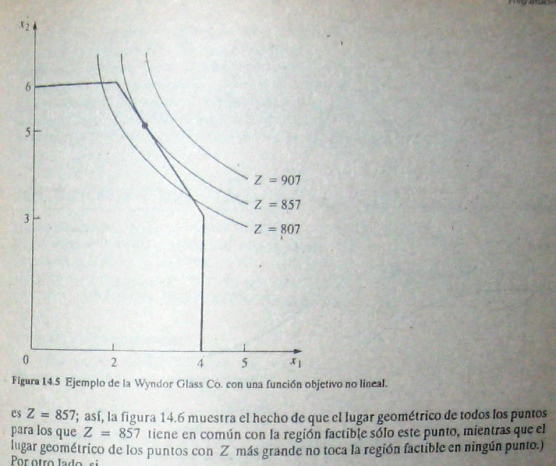
La figura 14.5 muestra lo que ocurre con este problema si los únicos cambios que se hacen al modelo de la sección 3.1 son que la segunda y tercera restricciones se sustituyen por la restricción no lineal 9x1² + 5x2² ≤ 216. Compárense las figuras 14.5 y 3.3. La solución óptima sigue siendo(x1, x2) = (2,6). Además, todavía se encuentra sobre la frontera de la región factible, pero no es una solución en un vértice. La solución óptima pudo haber sino una solución factible en un vértice con una función objetivo diferente (verifíquese Z = 3x1 + x2), pero el hecho de que no necesita serlo significa que ya no se puede aprovechar la gran simplificación utilizada en programación lineal que permite limitar la búsqueda de una solución óptima nada más a la olucione factibles en los vértices.
martes, 8 de septiembre de 2015
Selección de una cartera de inversiones riesgosa (IV)
lunes, 7 de septiembre de 2015
Selección de una cartera de inversiones riesgosa (III)
en donde Pj es el precio de cada acción tipo j y B es la cantidad de dinero presupuestada para la cartera. Si se hacen ciertas suposiciones sobre la función de utilidad del inversionista (medida del valor relativo para el inversionista de lo distintos rendimientos totales), se puede demostrar que una solución óptima para este modelo de programación no lineal maximiza la utilidad esperada del inversionista.
domingo, 6 de septiembre de 2015
Selección de una cartera de inversiones riesgosa (II)
sábado, 5 de septiembre de 2015
Selección de una cartera de inversiones riesgosa (I)
viernes, 4 de septiembre de 2015
jueves, 3 de septiembre de 2015
Problema de transporte con descuentos por volumen en los precios de embarque
miércoles, 2 de septiembre de 2015
El problema de la mezcla de productos con elasticidad en los precios (II)
Otra razón por la que pueden surgir no linealidades en la función objetivo es que los costos marginales al producir otra unidad más de un producto dado pueden variar con el nivel de producción. Por ejemplo, el costo marginal puede decrecer cuando aumente el nivel de producción, gracias al efecto de una curva de aprendizaje (mayor eficiencia con más experiencia). Por otro lado, pueden aumentar a causa de ciertas medidas especiales, como tiempos extra o instalaciones de producción más costosas, necesarias para aumentar la producción.
La no linealidad también puede surgir en las funciones de restricción gi(x) en forma bastante parecida. Por ejemplo, si existe una restricción de presupuesto sobre el costo total de producción, la función de costo será no lineal si el costo marginal de producción varía como se acaba de describir. Para restricciones sobre otro tipo de recursos, gi(x) será no lineal siempre que el uso del recurso correspondiente no sea estrictamente proporcional a los niveles de los respectivos productos.
martes, 1 de septiembre de 2015
lunes, 31 de agosto de 2015
El problema de la mezcla de productos con elasticidad en los precios (I)
domingo, 30 de agosto de 2015
Algunas aplicaciones
sábado, 29 de agosto de 2015
Programación no lineal (II)
viernes, 28 de agosto de 2015
Programación no lineal (I)
De una manera general, el problemade programación no lineal consiste en encontrar x = (x1, x2,......xn) para
Maximizar f(x).
sujeta a gi(x) ≤ bi, para i = 1,2,......m
x ≥ 0,
en donde f(x) y las gi(x) son funciones dadas de n variables de decisión.
jueves, 27 de agosto de 2015
Conclusión Programación Entera (III)
Recientemente se han llevado a cabo muchas investigaciones con el fin de desarrollar algoritmos para programación entera no lineal, área cuyo estudio continúa muy activo.
miércoles, 26 de agosto de 2015
Conclusión Programación Entera (II)
A veces los problemas prácticos de PE son tan grandes que no se pueden resolver ni con los últimos algoritmos. En estos casos, es común aplicar el método símplex nada más a la soltura de PL y después redondear la solución a una solución entera factible. Este enfoque no suele ser satisfactorio porque puede ser difícil (o imposible) encontrar una solución etera factible de esta manera. Y aun encontrándola, puede estar muy alejada del óptimo. Esto es cierto en especial cuando se manejan variables binarias e incluso variables enteras generales con valores pequeños.
martes, 25 de agosto de 2015
Conclusión Programación Entera (I)
En la actualidad es común que se disponga de paquetes de computadora para algoritmos de programación entera en el software de programación matemática. EStos algoritmos casi siempre se basan en la técnica de ramificación y acotamiento o en alguna variación de ésta.
lunes, 24 de agosto de 2015
Programación Entera Desarrollos recientes (IX)
domingo, 23 de agosto de 2015
Programación Entera Desarrollos recientes (VIII)
El nuevo enfoque algorítmico presentado en las referencias selectas 1,4 y 13 implica la generación de muchas cortaduras en forma parecida antes de aplicar las técnicas de ramificación y acotamiento. Los resultados al incluir cortaduras pueden ser importantes para estrechar las solturas de PL. Por ejemplo, para el problema de prueba con 2756 variables binarias del artículo de 1983, se generaron 326 cortaduras. El resultado fue que la distancia entre el valor de Z de la solución óptima de la soltura de PL del problema completo de PEB y el valor de Z de la solución óptima del problema se redujo en un 98%. En casi la mitad de los problemas se obtuvieron resultados similares.
sábado, 22 de agosto de 2015
Programación Entera Desarrollos recientes (VII)
6x1 + 3x2 + 5x3 + 2x4 ≤ 10
Ahora nótese que las restricciones binarias y esta restricción juntas implican que
x1 + x2 +x4 ≤ 2.
viernes, 21 de agosto de 2015
Programación Entera Desarrollos recientes (VI)
Se ha comprobado que el uso de la computadora para llevar a cabo estas ideas y otras parecidas en forma automática es de gran ayuda para acelerar un algoritmo. Sin embargo, una técnica todavía más importante es la generación de planos cortantes. Una cortadura para un problema de PE es una nueva restricción que elimina algunas soluciones factibles de la soltura de PL original, incluso su solución óptima. El propósito de agregar una nueva restricción con esta propiedad es estrechar la soltura de PL, estrechando con esto la cota obtenida en el paso de acotamiento de la técnica de ramificación y acotamiento. Al estrechar la soltura de PL se incrementa la posiblidad de que su solución óptima sea factible (y por lo tanto óptima) para el problema de PE, con lo que e mejoraría la prueba de sondeo 3.
jueves, 20 de agosto de 2015
Programación Entera Desarrollos recientes (V)
3x1 + 2x2 ≤ 2 ⇒ x1 = 0
3x3 - 2x4 ≤ -1 ⇒ x3 = 0 y x4 = 1
de manera que se puede eliminar la variable del modelo (después de sustituir su valor fijo). una restricción funcional puede ser redundante a las restriciones binarias, por ejemplo,
3x1 + 2x2 ≤ 6,
y puede eliminarse. Es posible estrechar una restricción funcional reduciendo algunos de sus coeficientes, debido a las restricciones binarias, por ejemplo,
4x1 + 5x2 + x3 ≥ 2 ⇒ 2x1 + 2x2 + x3 ≥ 2
miércoles, 19 de agosto de 2015
Programación Entera Desarrollos recientes (IV)
Aunque está más allá del alcance de este libro describir con detalle el nuevo enfoque algorítmico, se dará una idea global breve. ( Se anima al lector a que la las referencias 1, 4 y 13 para mayor información).
Este enfoque utiliza una combinación de los tres tipos de técnicas: 1) preprocesado automático del problema, 2) generación de planos cortantes o cortaduras y 3) técnicas de ramificación y acotamiento. El lector está familiarizado con la técnicas de ramificación y acotamiento y no se profundizará más en las versiones más elaboradas que se incorporan aquí. A continuación e da una introducción conceptual sobre los otros dos tipo de técnicas que usan.
martes, 18 de agosto de 2015
Programación Entera Desarrollos recientes (III)
Por otro lado, cada nuevo cambio algorítmico en investigación de operaciones genera siempre una renovación en la actividad de investigación para desarrollar y refinar el nuevo enfoque. Sin duda se verán más frutos de la intensificación de esta actividad en programación entera durante la siguiente década. Quizá a través de la investigación se puedan disminuir las diferencias que existen en cuanto a la eficiencia entre lo algoritmos de programación entera y los de programación líneal.
lunes, 17 de agosto de 2015
Programación Entera Desarrollos recientes (II)
Sin embargo, estos dos artículos se limitana PEB pura. ES bastante común que en los problemas de PE que surgen en la práctica todas las variables restringidas a valores enteros sean binarias, pero muchos de estos problemas son de PEBmixta. Lo que e necesitaba con desesperación era una forma de extender este mismo tipo de algoritmo a la PEBmixta. Esto ocurrió en el artículo de 1987 publicado por Tony Van Roy y Laurence Wolsey de Bélgica. Una vez más, se resolvían con éxito problemas de tamaño muy grande (hasta cerca de mil variables binarias y un gran número de variable continuas). Una vez más, este artículo ganó un prestigiado premio, el Orchard-Hays Price otorgado por la Mathematical Programming Society.
domingo, 16 de agosto de 2015
Programación Entera Desarrollos recientes (I)
Para dar una mejor perspectiva sobre este progreso, considérense los antecedentes históricos. A fines de la década de 1960 y principios de la de 1970 hubo un cambio grande con el desarrollo y refinamiento del enfoque de ramificación y acotamiento. Después, todo siguió igual; se podían resolver en forma muy eficiente problemas relativamente pequeños (muy por debajo de las cien variables) pero aún un pequeño aumento en el tamaño del problema podía causar una explosión en el tiempo de cálculos más allá de los límites factibles. Se hacían pocos progresos para vencer este crecimiento exponencial en el tiempo de computación; cuando el tamaño del problema aumentaba, muchos problemas importantes que surgían en la práctica no se podían resolver.
sábado, 15 de agosto de 2015
Ejemplo Resumen del algoritmo de ramifiación y acotamiento de PEM (X)
Incumbente = (0, 0, 2, 1/2) con Z* = 13(1/2)
Con esta Z* se vuelve a realizar la prueba de sondeo 1 al otro subproblema (subproblema 4) y pasa la prueba, ya que su cota de 12(1/6) es ≤ Z*.
Esta iteración tuvo éxito en sondear de la tres maneras posibles. Lo que es más, ya no hay subproblemas restantes, por lo tanto la solución incumbente actual es óptima.
Solución óptima = (0, 0, 2, 1/2), con Z* = 13(1/2).
EStos resultados se resumen en el árbol de soluciones de la figura 13.10.
viernes, 14 de agosto de 2015
Ejemplo Resumen del algoritmo de ramifiación y acotamiento de PEM (IX)
Iteración 3
De los dos subproblemas restantes (3 y 4) que se crearon al mismo tiempo, se selecciona el que tiene la cota más grande (subproblema 3, con 14(1/6) > 12(1/6) para la siguiente ramificación). Como x1 = 5/6 tiene un valor no entero en la solución óptima de la soltura de PL de su subproblema, x1 se convierte en la variable de ramificación. (Obsérvese que x1 es ahora una variable de ramificación recurrente, pues también se seleccionó en la iteración 1.) Esto conduce a los siguientes subproblemas:jueves, 13 de agosto de 2015
Ejemplo Resumen del algoritmo de ramifiación y acotamiento de PEM (VIII)
Soltura de PL del subproblema 3: (x1, x2, x3, x4) = (5/6, 1, 11/6, 0), con Z = 14(1/6)
Cota para el subproblema 3: Z ≤ 14(1/6)
Soltura de PL del subproblema 4: (x1, x2, x3, x4) = (5/6, 2, 11/6, 0), con Z = 12(1/6)
Cota para el subproblema 4: Z ≤ 12(1/6)
Como ambas soluciones existen (soluciones factibles) y tienen valores no enteros para variables restringidas a enteros, ninguno de los subproblemas se sondea. (La prueba I no es operativa, puesto que todavía Z* = - ∞, hasta que se encuentre la primera solución de apoyo.)
El árbol de solución hasta este punto se da en la figura 13.9.