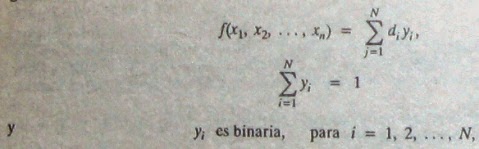Ahora es necesario obtener, para cada subproblema, una cota que muestre qué tan buena puede ser su mejor solución factible. La forma más común para hacer esto es resolver rápidamente una soltura sencilla del subproblema. Casi siempre, una soltura de un problema se obtiene elininando ("soltando") un conjunto de restricciones que hacen que el problema sea difícil de resolver. En los problemas de PE las restricciones de más dificultad son las que requieren que las variables sean enteras. Entonces, la soltura que más se usa es la soltura de PL que elimina este conjunto de restricciones.
Trabajando con el ejemplo, considérese primero el problema completo dado en la sección 13.1. Su soltura de PL se obtiene al eliminar el último renglón del modelo (xj es entera, para j = 1,2,3,4) pero conservando las restricciones de xj ≤ 1 y xj ≥ 0. Al aplicar el método símplex para resolver esta soltura de PL se obtiene su solución óptima.
(x1, x2, x3, x4 ) = (5/6, 1, 0, 1), con Z = 16(1/2)
martes, 30 de junio de 2015
Acotamiento (I)
lunes, 29 de junio de 2015
Ramificación (III)
En otros problemas de programación entera, en donde los valores enteros pueden tener más de dos variables posibles, la ramificación se puede hacer estableciendo la variable de ramificación igual a sus respectivos valores individuales, con lo que se crean más de dos subproblemas. Otro buen enfoque es especificar el intervalo de valores (por ejemplo, xj ≤ 2 o xj ≥ 3) para la variable de ramificación para cada nuevo subproblema. Este es el enfoque que se usa en el algoritmo que se presenta en la sección 13.5
domingo, 28 de junio de 2015
Ramificación (II)
La figura 13.2 muestra esto con una división (ramificación) en subproblemas, mediante un árbol (definido en la sección 10.2) con ramas (arcos) desde todos los nodos (correspondientes al problema completo que contiene todas las soluciones factibles) a los dos nodos correspondientes a los dos subproblemas. Este árbol que hará *crecer sus ramas* en cada interación se conoce como el árbol de soluciones (o árbol de enumeración) para el algortimo. La variable que se usa para hacer la ramificación en una iteración al asignarle valores (como con x1) se llama variable de ramificación.
Más adelante se verá que uno de estos subproblemas se puede vencer (sondear) de inmediato, mientas que el otro requiere una nueva división en subproblemas más pequeños estableciendo x2 = 0 o x2 = 1, etc.
Más adelante se verá que uno de estos subproblemas se puede vencer (sondear) de inmediato, mientas que el otro requiere una nueva división en subproblemas más pequeños estableciendo x2 = 0 o x2 = 1, etc.
sábado, 27 de junio de 2015
Ramificación (I)
Cuando se manejan variables binarias, la forma más sencilla de partir el conjunto de soluciones factibles es fijar el valor de una variable (por ejemplo, x1) en x1 = 0 para un subconjunto y en x1 = 1 para el otro. Al hacer esto en el ejemplo prototipo, el problema completo queda dividido en dos subproblemas más pequeños, como sigue:
Subproblema 1: (x1 = 0)
Maximizar Z = 5x2 + 6x3 + 4x4
Subproblema 1: (x1 = 0)
Maximizar Z = 5x2 + 6x3 + 4x4
viernes, 26 de junio de 2015
Técnica de ramificación y acotamiento y sus aplicaciones a la programación entera binaria
Como cualquier problema acotado de programación entera pura, tiene sólo un número finito de soluciones factibles, resulta natural considerar el uso de algun tipo de procedimiento de enumeración para encontrar una solución óptima. Desafortunadamente, como ya se dijo, este número finito puede ser, y casi siempre lo es, muy grande, por lo que es imperativo que cualquier procedimiento de enumeración de estructura con habilidad para que sólo sea necesario examinar una pequeña fracción de estas soluciones factibles. Por ejemplo, la programación dinámica (véase el capítulo) proporciona un procedimiento de este tipo para muchos problemas que tienen un número finito de soluciones factibles (aunque no es especialmente eficiente para la mayor parte delos problemas de PE) Otro enfoque de este tipo lo proporciona la técnica de ramificación y acotamiento. Esta técnica y algunas variaciones se han aplicado con cierto éxito a diversos problemas de investigación de operaciones, pero es más conocida por sus aplicaciones a los problemas de programación entera.
La idea básica en la que se apoya esta técnica se divide y vencerás. Como es demasiado complicado resolver directamente el problema original "grande", se divide en subproblemas cada vez más pequeños hasta que estos se puedan vencer. La división (ramificación) se hace mediante una partición del conjunto completo de soluciones factibles en subconjuntos más pequeños. La consulta (sondeo) se hace en parte acotando la mejor solución en el subconjunto y después descartando los subconjuntos cuya cota indique que no es posible que contenga una solución óptima.
Ahora se describirá cada uno de estos pasos básicos -ramificación, acotamiento y sondeo - y se ilustrarán aplicando un algoritmo de ramificación y acotamiento al ejemplo prototipo (el problema de California Manufacturing Co.) que se presentó en la sección 13.1.
La idea básica en la que se apoya esta técnica se divide y vencerás. Como es demasiado complicado resolver directamente el problema original "grande", se divide en subproblemas cada vez más pequeños hasta que estos se puedan vencer. La división (ramificación) se hace mediante una partición del conjunto completo de soluciones factibles en subconjuntos más pequeños. La consulta (sondeo) se hace en parte acotando la mejor solución en el subconjunto y después descartando los subconjuntos cuya cota indique que no es posible que contenga una solución óptima.
Ahora se describirá cada uno de estos pasos básicos -ramificación, acotamiento y sondeo - y se ilustrarán aplicando un algoritmo de ramificación y acotamiento al ejemplo prototipo (el problema de California Manufacturing Co.) que se presentó en la sección 13.1.
jueves, 25 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (IX)
Uno de los algortimos más populares de programación entera es la técnica de ramificación y aontecimientoy las ideas relacionadas con la enumeración implícita de las soluciones factibles enteras, cuyos enfoques se analizarán aquí. La siguiente sección presenta la técnica de ramificación y acotamiento en un contexto general. La sección 13.5 describe otro algoritmo del mismo tipo para problemas de programación entera mixta.
miércoles, 24 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (VIII)
A causa de estos riesgos una mejor forma de tratar con problemas de programación entera grandes es usar uno de los algortimos heurísticos disponibles. Estos algoritmos son muy eficientes para problemas grandes, pero no garantizan que se llegue a una solución óptima. Sin embargo, tienden a ser considerablemente más efectivos para encontrar excelentes soluciones factibles que el enfoque de redondeo que se acaba de analizar.
Por ahora se dispone de un gran número de algoritmos para pequeños problemas de programación entera que deben resolverse hasta llegar al óptimo. Por desgracia, ninguno posee eficiencia computacional que se pueda siquiera comparar con el método símplex (excepto los tipos especiales de problemas). El desarrollo de algoritmos de programación entera sigue siendo un tema de investigación. Por fortuna, durante la última parte de la decáda de 1980 se hicieron algunos adelantos y se esperan más progresos para la siguiente década. Estos adelantos recientes se analizarán en la sección 13.6.
Por ahora se dispone de un gran número de algoritmos para pequeños problemas de programación entera que deben resolverse hasta llegar al óptimo. Por desgracia, ninguno posee eficiencia computacional que se pueda siquiera comparar con el método símplex (excepto los tipos especiales de problemas). El desarrollo de algoritmos de programación entera sigue siendo un tema de investigación. Por fortuna, durante la última parte de la decáda de 1980 se hicieron algunos adelantos y se esperan más progresos para la siguiente década. Estos adelantos recientes se analizarán en la sección 13.6.
martes, 23 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (VII)
Aun cuando la solución óptima se pueda redondear con éxito, todavía queda otro peligro. No existe garantía de que esta solución redondeada sea la solución óptima de programación entera. En realidad, puede incluso que se encuentre muy lejos del óptimo en términos del valor de la función objetivo. El siguiente problema ejemplifica esto:
lunes, 22 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (VI)
Como, en general, es mucho más difícil resolver los problemas de programación entera que los de programación lineal, a veces es tentador usar el procedimiento aproximado y aplicar el método símplex a la soltura de PL y después redondear los valores no enteros a enteros en la solución obtenida. Este enfoque puede ser adecuado en algunas aplicaciones, en especial si los valores de las variables son tan grandes que el redondeo causa un error muy pequeño; pero debe tenerse cuidado al hacer esto, pues hay dos riesgos que se corren
Un problema es que la solución óptima de programación lineal no necesariamente es factible después de redondearla. Con frecuencia es difícil decidir en qué sentido redondear para conservar la factibilidad. Puede ser necesario incluso cambiar el valor de algunas variables en una o más unidades después de redondear. Para ilustrar esto, supóngase que algunas restricciones son:
y que el método símplex ha identificado la solución óptima para la soltura de PL como x1 = 6(1/2), x2 = 10. Nótese que es imposible redondear x1 a 6 o a 7 ( o a ningún otro entero) y conservar la factibilidad. Esta factibilidad sólo se puede conservar si también se cambia el valor entero de x2. Es fácil imaginar la complejidad a la que se puede llegar con este tipo de dificultades cuando se tienen decenas o cientos de restricciones y variables.
Un problema es que la solución óptima de programación lineal no necesariamente es factible después de redondearla. Con frecuencia es difícil decidir en qué sentido redondear para conservar la factibilidad. Puede ser necesario incluso cambiar el valor de algunas variables en una o más unidades después de redondear. Para ilustrar esto, supóngase que algunas restricciones son:
-x1 + x2 ≤ 3(1/2)
x1 + x2 ≤ 16(1/2)
y que el método símplex ha identificado la solución óptima para la soltura de PL como x1 = 6(1/2), x2 = 10. Nótese que es imposible redondear x1 a 6 o a 7 ( o a ningún otro entero) y conservar la factibilidad. Esta factibilidad sólo se puede conservar si también se cambia el valor entero de x2. Es fácil imaginar la complejidad a la que se puede llegar con este tipo de dificultades cuando se tienen decenas o cientos de restricciones y variables.
domingo, 21 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (V)
Aunque toda esta simplificación no es usual, con frecuencia los problemas de programación entera que surgen en la práctica tiene alguna estructura especial que se puede aprovechar para simplificarlos. A veces se pueden resolver con éxito versiones muy largas de estos problemas. Cada vez son más importantes los algortimos de propósitos especiales que están elaborados específicamente para explotar ciertos tipos de estructuras especiales en programación entera.
Entonces, los dos factores determinantes de la dificultad computacional de un problema de PE son 1) el número de variables enteras y 2) la estructura del problema. Esta situación es opuesta a la de programación lineal, en donde el número de restricciones funcionales es mucho más importante que el número de variables. En programación entera, el número de restricciones tiene alguna importancia (en especial, si se van a resolver las solturas de PL), pero es estrictamente secundario para los otros dos factores. De hecho, existen casos en los que aumentar el número de restricciones disminuye el tiempo de cálculo ya que se reduce el número de soluciones factibles. En los problemas de PEM es el número de variables enteras y no el número total de variables el que es importante, pues las variables continuas casi no tienen efecto sobre el esfuerzo computacional.
sábado, 20 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (IV)
Aunque, sin duda, casi siempre es accidental que la solución óptima de la soltura de PL sea entera de hecho, existen varios tipos especificos de problemas de PE para los que este resultado se puede garantizar. Ya se vieron dos de estos casos especiales en los capitulos 7 y 10, estos son el problema de flujo de costo mínimo (con parámetros enteros) y sus casos especiales (el problema de transporte, el problema de trasbordo, el problema de asignación, el problema de la ruta más corta, y el problema del flujo máximo). La razón por la que se puede dar esta garantía es la estructura especial que poseen estos tipos particulares de problemas, que asegura que toda solución factible es entera, como se estableció en la propiedad de soluciones enteras dada en las secciones 7.1 y 10.6. Por ello, estos tipos especiales de problemas de programación entera se pueden manejar como problemas de programación lineal (que es el motivo por el que tres de ellso aparecen en el capitulo 7) ya que se pueden resolver completamente aplicando las versiones simplificadas del método símplex.
viernes, 19 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (III)
Existe una situación especial en la que no es más difícil resolver el problema de programación entera que resolver una vez su soltura de PL aplicando el método símplex; esta situación es aquélla en la que la solución a la soltura de PL satisface la restricción de valores enteros.
Cuando ocurre esto, la solución también debe ser óptima para el problema de programación entera, ya que se trata de la mejor solución entre todas las soluciones de la soltura de PL, que incluye todas las soluciones factibles del problema de programación entera. Entonces, es normal que un algoritmo de programación entera comience con la aplicación del método símplex a su soltura de PL, para verificar si tiene lugar este casual acontecimiento.
Cuando ocurre esto, la solución también debe ser óptima para el problema de programación entera, ya que se trata de la mejor solución entre todas las soluciones de la soltura de PL, que incluye todas las soluciones factibles del problema de programación entera. Entonces, es normal que un algoritmo de programación entera comience con la aplicación del método símplex a su soltura de PL, para verificar si tiene lugar este casual acontecimiento.
jueves, 18 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (II)
La segunda falacia es que al eliminar algunas soluciones factibles (las o enteras) de un problema de programación lineal, será más fácil de resolverlo. Todo lo contrario: sólo cuando todas estas soluciones factibles están ahí, se puede garantizar (véase la sección 5.1) que existe una solución factible en el vértice (solución básica factible) que es óptima para el problema completo. Esta garantía es la clave de la extraordinaria eficiencia del método símplex. Como resultado, en general es mucho más sencillo resolver los problemas de programación líneal que los de programación entera.
ES lógico, entonces, que la mayor parte de los buenos algoritmos de programación entera incorporen el método simplex (o el método símplex dual) lo más que puedan, y relacionen partes del problema de PE bajo consideración con el problema correspondiente de programación líneal (es decir, el mismo problema con la restricción de valores enteros eliminada). Para cualquier problema dado de programacion entera, el problema correspondiente de programación líneal se conoce como su soltura de PL. El algortimo que se presenta en las dos secciones siguientes ilustra cómo se puede usar una sucesión de solturas de PL para porciones de un problema de programación entera, con objeto de resolver de manera eficiente un problema completo de PE.
ES lógico, entonces, que la mayor parte de los buenos algoritmos de programación entera incorporen el método simplex (o el método símplex dual) lo más que puedan, y relacionen partes del problema de PE bajo consideración con el problema correspondiente de programación líneal (es decir, el mismo problema con la restricción de valores enteros eliminada). Para cualquier problema dado de programacion entera, el problema correspondiente de programación líneal se conoce como su soltura de PL. El algortimo que se presenta en las dos secciones siguientes ilustra cómo se puede usar una sucesión de solturas de PL para porciones de un problema de programación entera, con objeto de resolver de manera eficiente un problema completo de PE.
miércoles, 17 de junio de 2015
Algunas perspectivas sobre la solución de problemas de programación entera (I)
Puede parecer que los problemas de programación entera son relativamente fáciles de resolver. Después de todo, los problemas de programación lineal se pueden resolver de una manera bastante eficiente, y la única diferencia es que la programación entera tiene muchas menos soluciones que considerar. De hecho, está garantizado que los problemas de PE pura con una región factible acotada tienen sólo un número finito de soluciones factibles.
Por desgracia, existen dos falacias en este tipo de razonamiento. Una es que el tener un número finito de soluciones factibles asegure que el problema se puede resolver. Los números finitos pueden ser astronómicamente grandes. Por ejemplo, considérese el caso de problemas sencillos de programación entera binaria. Si se tienen n variables, existen 2^n soluciones que se deben tomar en cuenta (en donde algunas de estas soluciones se pueden descartar por violar las restricciones funcionales). Entonces, cada vez que n se aumenta en uno, el número de soluciones se duplica. Este patrón se llama el crecimiento exponencial de la dificultad del problema. Con n =10, se tienen más de mil soluciones (1024); con n = 20, son más de un millón; con n = 30 resultan más de mil millones, y así sucesivamente; por eso, aun las computadoras más eficientes son incapaces de realizar una enumeración exhaustiva (que verifique la factibilidad de cada solución y, si es posible, calcular el valor de la función objetivo) para problemas de PEB con unas cuantas docenas de variables, sin mencionar los problemas de PE general con el mismo número de variables enteras. Se cuenta con algunos algoritmos elaborados, como los que se desarrollan en las secciones siguientes, que pueden llevar a cabo un mejor trabajo. En la sección 13.6 se explica cómo algunos algoritmos desarrollados recientemente han resuelto con éxito ciertos problemas muy grandes de PEB (de hasta 2756 variables). Sin embargo, debido al crecimiento exponencial, incluso los mejores algoritmos no garantizan la solución de todos los problemas relativamente pequeños (con menos de cien variables binarias o enteras.)
martes, 16 de junio de 2015
Representación binaria de variables enteras en general (IV)
Si se trata de un problema de programación entera en el que todas las variables son enteras generales (acotadas) sería posible usar esta misma técnica para reducirlo a un problema de PEB. Sin embargo, esto casi nunca es aconsejable debido a la explosión en el número de variables. En general, aplicar un buen algoritmo de PE al modelo original será más eficiente que aplicar un buen algoritmo de PEB a un modelo mucho más grande.
En términos generales, con todas las posibilidades de formulación con variables binarias auxiliares que se presentaron en esta sección, es necesario hacer notar una precaución que debe tenerse. Algunas veces, este enfoque requiere que se agregue un número relativamente grande de variables,lo que puede hacer que el modelo se vuelva no factible computacionalmente. De hecho, como se explica en las siguiente secciones, se pueden tener problemas con menos de cien variables binarias.
En términos generales, con todas las posibilidades de formulación con variables binarias auxiliares que se presentaron en esta sección, es necesario hacer notar una precaución que debe tenerse. Algunas veces, este enfoque requiere que se agregue un número relativamente grande de variables,lo que puede hacer que el modelo se vuelva no factible computacionalmente. De hecho, como se explica en las siguiente secciones, se pueden tener problemas con menos de cien variables binarias.
lunes, 15 de junio de 2015
Representación binaria de variables enteras en general (III)
DEspués de sustituir estas expresiones por las variables respectivas en todas las restricciones funcionales y en la función objetivo, las dos restricciones funcionales que se establecieron se convierten en:
domingo, 14 de junio de 2015
Representación binaria de variables enteras en general (II)
Por ejemplo, supóngase que un problema de PE tiene sólo dos variables enteras generales, x1 y x2 y muchas variables binarias, y que las restricciones funcionales incluyen
sábado, 13 de junio de 2015
Representación binaria de variables enteras en general (I)
Supóngase que se tiene un problema de programación entera pura en el que la mayoría de las variables son binarias, pero la presencia de algunas variables enteras generales evita que se pueda usara el eficiente algoritmo de programación entera binaria que ahora se conoce. Una manera de salvar esta dificultad es usar la representación binaria para cada una de estas variables enteras generales,. En particular, si las cotas de una variable entera x son;
en donde las variables yi son variables binarias (auxiliares). Si se sustituye esta representación binaria por cada variable entera general (con un conjunto diferente de variables binarias auxiliares para cada una), el problema completo se reduce a un modelo de PE.
en donde las variables yi son variables binarias (auxiliares). Si se sustituye esta representación binaria por cada variable entera general (con un conjunto diferente de variables binarias auxiliares para cada una), el problema completo se reduce a un modelo de PE.
viernes, 12 de junio de 2015
Problemas de costo fijo (V)
Si las xj también estuvieran restringidas a valores enteros, entonces éste sería un problema de programación entera pura.
Para ilustrar este enfoque, véase de nuevo en la sección 3.4 el problema de la contaminación ambiental que enfrenta la Nori & Leets Co. El primer método de abatimiento que se consideró (aumentar la altura de las chimeneas) en realidad significaría un enorme costo fijo para poder realizar cualquier aumento, además de un costo variable que en esencia sería proporcional al aumento. Después de una conversión al costo anual equivalente utilizado en la formulación, este cargo fijo sería de $2 000 000 por cada uno de los altos hornos y los hornos de hogar abierto, mientras que los costos variables son los mismos que se identificaron en la tabla 3.14. Así, en la notación anterior, k1 = 2, k2 = 2, c1 = 8 y c2 = 10. Como los otros métodos de abatimiento no implican cargos fijos, kj = 0 para j = 3, 4, 5, 6. Por lo tanto la nueva formulación de programación entera mixta de este problema es
Para ilustrar este enfoque, véase de nuevo en la sección 3.4 el problema de la contaminación ambiental que enfrenta la Nori & Leets Co. El primer método de abatimiento que se consideró (aumentar la altura de las chimeneas) en realidad significaría un enorme costo fijo para poder realizar cualquier aumento, además de un costo variable que en esencia sería proporcional al aumento. Después de una conversión al costo anual equivalente utilizado en la formulación, este cargo fijo sería de $2 000 000 por cada uno de los altos hornos y los hornos de hogar abierto, mientras que los costos variables son los mismos que se identificaron en la tabla 3.14. Así, en la notación anterior, k1 = 2, k2 = 2, c1 = 8 y c2 = 10. Como los otros métodos de abatimiento no implican cargos fijos, kj = 0 para j = 3, 4, 5, 6. Por lo tanto la nueva formulación de programación entera mixta de este problema es
jueves, 11 de junio de 2015
Problemas de costo fijo (IV)
miércoles, 10 de junio de 2015
Problemas de costo fijo (III)
Por tanto, se puede pensar que las yj son decisiones contingentes parecidas (pero no idénticas) a las que se consideraron en la sección 13.1. Sea M un número positivo muy grande que excede el máximo valor factible de cualquiera de las xj (j = 1,2.......,n). Entonces, las restricciones
martes, 9 de junio de 2015
Problemas de costo fijo (II)
Para formular el modelo completo, supóngase que existen n actividades, cada una con la estructura de costo anterior (con kj ≥ 0 en todos los casos y kj > 0 para alguna j = 1, 2,......n), y que el problema es
o no se representa por una variable binaria uj, de manera que
o no se representa por una variable binaria uj, de manera que
lunes, 8 de junio de 2015
Problemas de costo fijo (I)
Es bastante común incurrir en un cargo de preparación o costo fijo cuando se emprende una actividad. Por ejemplo, un cargo así ocurre cuando se inicia una corrida de producción para fabricar un lote pequeño de un producto en particular y deben prepararse las instalaciones de producción que se requieren. En tales casos, el costo total de la actividad es la suma de un costo variable relacionado con el nivel de la actividad y el costo fijo en el que se incurre para iniciar la actividad. Con frecuencia, el costo variable será, por lo menos a grandes rasgos, proporcional al nivel de la actividad. Si lo es, el costo total de la actividad (por ejemplo, j) se puede representar por una función de la forma
en donde xj denota el nivel de actividad j (xj ≥ 0), kj denota el costo fijo y cj denota el costo de cada unidad incremental. Si no fuera por el costo fijo kj, esta estructura de costo sugeriría la posibilidad de una formulación de programación líneal para determinar los niveles óptimos de las actividades competitivas. Por fortuna, aun si se incluyen la k, se puede usar programación entera.
domingo, 7 de junio de 2015
Funciones con N valores posibles (III)
Para ilustrar cómo puede surgir un caso de este tipo, reconsidérese el problema de la Wyndor Glass Co. que se presentó en la sección 3.1. En la actualidad, el 18% de la capacidad total de la planta no se usa y está disponible para los dos nuevos productos o para ciertos productos futuros que muy pronto estarán listos para producción. Con el fin de dejar cualquier capacidad restante en forma de bloques utilizables para estos productos futuros, la administración desea imponer la restricción de que la capacidad usada por los dos nuevos productos actuales sea el 6% o el 12% o el 18%. Entonces, la tercera restricción del modelo original (3x1 + 2x2 ≤ 18) debe cambiar a
El modelo completo para esta nueva versión del problema consiste, entonces, en el modelo original (véase la sección 3.1), más este nuevo conjunto de restricciones. Esta situación conduce a una formulación de programación entera muy clara.
El modelo completo para esta nueva versión del problema consiste, entonces, en el modelo original (véase la sección 3.1), más este nuevo conjunto de restricciones. Esta situación conduce a una formulación de programación entera muy clara.
sábado, 6 de junio de 2015
Funciones con N valores posibles (II)
La formulación equivalente de programación entera para este requerimiento es la siguiente:
con lo que este nuevo conjunto de restricciones sustituye el requerimiento que se hizo al establecer el problema. Este conjunto de restricciones proporciona una formulación equivalente puesto que exactamente una de las yi debe ser igual a 1 y las otras deben ser iguales a cero, así que se está escogiendo justo una di como el valor de la función. En este caso existen N preguntas como con respuesta sí o no, a saber, debe ser di,el valor escogido (i = 1,2......,N). Como la yi respectiva representa estas decisiones si o no, la segunda restricción las hace alternativas mutuamente excluyentes.
con lo que este nuevo conjunto de restricciones sustituye el requerimiento que se hizo al establecer el problema. Este conjunto de restricciones proporciona una formulación equivalente puesto que exactamente una de las yi debe ser igual a 1 y las otras deben ser iguales a cero, así que se está escogiendo justo una di como el valor de la función. En este caso existen N preguntas como con respuesta sí o no, a saber, debe ser di,el valor escogido (i = 1,2......,N). Como la yi respectiva representa estas decisiones si o no, la segunda restricción las hace alternativas mutuamente excluyentes.
viernes, 5 de junio de 2015
Funciones con N valores posibles (I)
Considérese la situación en la que se requiere que una función dada tome cualquiera de N valores dados. Denótese este requisito por
jueves, 4 de junio de 2015
Restricciones de una u otra (IV)
Después, con la misma lógica que para el caso anterior, se encuentra que una formulación equivalente del requerimiento de que K de estas restricciones se deben cumplir es:
en donde M es un número positivo muy grande, Como las restricciones sobre las yi garantizan que K de estas variables serán igual a cero y las restantes serán igual a 1, K de las restricciones originales no cambiarán y el resto, de hecho será eliminado. Con objeto de elegir cuáles K de estas restricciones deben retenerse, se aplica el algoritmo apropiado al problema completo para que encuentre una solución óptima para todas estas variables simultáneamente.
en donde M es un número positivo muy grande, Como las restricciones sobre las yi garantizan que K de estas variables serán igual a cero y las restantes serán igual a 1, K de las restricciones originales no cambiarán y el resto, de hecho será eliminado. Con objeto de elegir cuáles K de estas restricciones deben retenerse, se aplica el algoritmo apropiado al problema completo para que encuentre una solución óptima para todas estas variables simultáneamente.
miércoles, 3 de junio de 2015
Deben cumplirse K de N restricciones (I)
Considérese la situación en la que el modelo completo incluye un conjunto de N restricciones posibles entre las que sólo K de ellas se deben cumplir. (Supóngase que K < N). Parte del proceso de optimización es elegir qué combinación de K restricciones permite que la función objetivo adquiera el mejor valor posible. Las (N-K) restricciones que no se eligen, de hecho, quedan eliminadas del problema, aun cuando por coincidencia las soluciones factibles puedan satisfacer algunas de ellas.
Este caso es una generalización directa del anterior para el que K = 1 y N = 2 Denótese las N posibles restricciones por
Este caso es una generalización directa del anterior para el que K = 1 y N = 2 Denótese las N posibles restricciones por
martes, 2 de junio de 2015
Restricciones de una u otra (III)
Como sólo una de estas dos preguntas tendrá una respuesta afirmativa, los respectivos términos binarios, y y (1-y), representan las decisiones de sí o no, de manera que y + (1 -y) = 1 (un sí) automáticamente. Si en lugar de esto se usan las variables binarias separadas y1 y y2 para representar estas decisiones de sí o no, entonces se necesita una restricción adicional y1 + y2 = 1, para hacerlas mutuamente excluyentes.
A continuación se da una presentación formal de este enfoque para un caso más general.
A continuación se da una presentación formal de este enfoque para un caso más general.
lunes, 1 de junio de 2015
Restricciones de una u otra (II)
Como la variable auxiliar y puede ser cero o 1, esta formulación garantiza que una de las restricciones originales se debe cumplir mientras que la otra queda, de hecho, eliminada. Este nuevo conjunto de restricciones se podría añadir a las otras restricciones del modelo completo para obtener un problema de programación entera pura o mixta (según si las xj son variables enteras o continuas).
Este enfoque se relaciona en forma directa con el análisis anterior sobre cómo expresar las relaciones combinatorias en términos de preguntas que se deben responder con sí o no. La relación combinatoria a la que se hace referencia concierne a la combinación de otras restricciones del modelo con la primera de las dos restricciones alternativas y después con la segunda. Cuál de estas dos combinaciones de restricciones es mejor (en términos del valor de la función objetivo que se puede lograr?) Si esta pregunta se hace en términos de sí o no, en realidad deben hacerse dos preguntas complementarias:
Este enfoque se relaciona en forma directa con el análisis anterior sobre cómo expresar las relaciones combinatorias en términos de preguntas que se deben responder con sí o no. La relación combinatoria a la que se hace referencia concierne a la combinación de otras restricciones del modelo con la primera de las dos restricciones alternativas y después con la segunda. Cuál de estas dos combinaciones de restricciones es mejor (en términos del valor de la función objetivo que se puede lograr?) Si esta pregunta se hace en términos de sí o no, en realidad deben hacerse dos preguntas complementarias:
Suscribirse a:
Entradas (Atom)