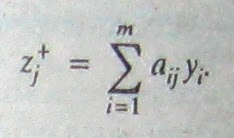Al agregar estos incrementos a las cantidades originales en la tabla símplex final (parte media de la tabla 6.18) se obtiene la tabla símplex revisada final (parte inferior de la tabla 6.18).
Este análisis incremental proporciona también una idea general útil, a saber, que los cambios de la tabla símplex final deben ser proporcionales a cada cambio en la tabla símplex final deben ser proporcionales a cada cambio en la tabla símplex inicial. En la siguiente sección se ejemplificará cómo esta propiedad permite usar la interpolación o extrapolación para determinar el intervalo de valores de un parámetros dado para el que la solución básica final permanece tanto factible como óptima.
Después de obtener la tabla símplex final revisada, se convierte la tabla en la forma apropiada de eliminación de Gauss (como sea necesario). En particular, la variable básica para el renglón i debe tener un coeficiente de 1 en ese renglón y cero en todos los demás renglones (inclusive renglón 0), para que la tabla esté en la forma apropiada para identificar y evaluar la solución básica actual. Por tanto, si los cambios violan este requisito (lo que puede ocurrir sólo si se cambiaron los coeficientes de una variable básica original), se deberán hacer los cambios necesarios para reestablecer esta forma. Esta restauración se hace con el método de eliminación de Gauss, es ecir, mediante aplicaciones sucesivas e la parte 3 del paso iterativo del método símplex como si cada variable que no cumple con el requisito fuera una variable entrante. Nótese que este proceso puede causar otros cambios en la columna del lado derecho, por lo que la solución básica actual se podrá leer en esta columna cuando se haya recuperado por completo la forma apropiada de eliminación de Gaus.
lunes, 31 de marzo de 2014
domingo, 30 de marzo de 2014
Esencia del análisis de sensibilidad (VIII)
En realidad, los cálculos para obtener la tabla símplex final se pueden simplificar de manera sustancial. Como ninguno de los coeficientes de x2 cambio en el modelo (o tabla símplex) original, ninguno de ellos puede cambiar en la tabla final, así se puede eliminar su cálculo. Algunos otros parámetros originales (a11, a21, b1, b3) tampoco cambiaron, entonces otro atajo consiste en calcular nada más los cambios incrementales en la tabla símplex final en términos de los cambios incrementales en la tabla inicial ignorando aquellos términos en la multiplicación de vectores o matrices que tuvieron un cambio de cero en la tabla inicial. En particular, los únicos cambios incrementales en la tabla símplex inicial son Δc1 = 1, Δa31= -1 y Δb2 =12, por tanto, estos son los únicos términos que tiene que considerarse. Esta simplificación se muestra en seguida, aparecerá un cero o un guión en el lugar de cada elemento para el que no se necesitó hacer el cálculo.
sábado, 29 de marzo de 2014
Esencia del análisis de sensibilidad (VII)
Estos coeficientes de las variables de holgura quedan necesariamente sin cambiar cuando se realizan las mismas operaciones algebraicas que originalmente realizó el método símplex porque los coeficientes de estas mismas variables en la tabla símplex inicial no cambian.
Sin embargo, como otras partes de la tabla símplex inicial cambiaron, habrá modificaciones en la tabla símplex final. Cuando se usan las fórmulas de la tabla 6.17, los números de la tabla símplex final se calculan como sigue:
La tabla símplex final revisada que resulta se muestra en al parte inferior de la tabla 6.18.
Sin embargo, como otras partes de la tabla símplex inicial cambiaron, habrá modificaciones en la tabla símplex final. Cuando se usan las fórmulas de la tabla 6.17, los números de la tabla símplex final se calculan como sigue:
La tabla símplex final revisada que resulta se muestra en al parte inferior de la tabla 6.18.
viernes, 28 de marzo de 2014
Esencia del análisis de sensibilidad (VI)
La tabla símplex inicial nueva que resulta se muestra en la parte superior de la tabla 6.18. Debajo se encuentra la tabla símplex final original (como se estableció antes en la tabla 4.8). Se dibujaron cuadros oscuros para marcar las partes de esta tabla final que definitivamente no se alteran con los cambios al modelo, a saber, los coeficientes de las variables de holgura tanto en el renglón 0 (y*) como en el resto de los renglones (S*). Así,
jueves, 27 de marzo de 2014
Esencia del análisis de sensibilidad (V)
Para llevar a cabo este procedimiento, se comienza por escribir los parámetros del modelo revisado en forma matricial:
miércoles, 26 de marzo de 2014
Esencia del análisis de sensibilidad (IV)
A manera de ilustración, supóngase que el modelo original de la Wyndor Glass Co. de la sección 3.1 se revisa según se muestra en el cuadro de la derecha.
Así, los cambios al modelo original son c1 =3 → 4, a31 = 3 → 4 y b2 = 12 → 24. La figura 6.2 muestra el efecto gráfico de estos cambios. Para el modelo original, el método símplex ya ha identificado la solución factible óptima en el vértice (2, 6) que se encuentra en la intersección de las dos fronteras de restricción que se muestran como líneas punteadas, 2x2 = 12 y 3x1 + 2x2 = 18. Ahora, la revisión del modelo ha cambiado ambas fronteras por las que se muestran con líneas oscuras, 2x2 = 24 y 2x1 + 2x2 = 18. En consecuencia, la solución factible en el vértice anterior (2,6) cambia ahora a la nueva intersección (-3,12) que es una solución no factible en un vértice para el modelo revisado. El procedimiento descrito en los parráfos anteriores encuentra este cambio algebraicamente (en la forma aumentada). Más aún, lo hace de manera muy eficiente aunque se trate de problemas grandes para los que el análisis gráfico es imposible.
Así, los cambios al modelo original son c1 =3 → 4, a31 = 3 → 4 y b2 = 12 → 24. La figura 6.2 muestra el efecto gráfico de estos cambios. Para el modelo original, el método símplex ya ha identificado la solución factible óptima en el vértice (2, 6) que se encuentra en la intersección de las dos fronteras de restricción que se muestran como líneas punteadas, 2x2 = 12 y 3x1 + 2x2 = 18. Ahora, la revisión del modelo ha cambiado ambas fronteras por las que se muestran con líneas oscuras, 2x2 = 24 y 2x1 + 2x2 = 18. En consecuencia, la solución factible en el vértice anterior (2,6) cambia ahora a la nueva intersección (-3,12) que es una solución no factible en un vértice para el modelo revisado. El procedimiento descrito en los parráfos anteriores encuentra este cambio algebraicamente (en la forma aumentada). Más aún, lo hace de manera muy eficiente aunque se trate de problemas grandes para los que el análisis gráfico es imposible.
martes, 25 de marzo de 2014
Esencia del análisis de sensibilidad (III)
Para escribir este procedimiento con más detalle, considérese la siguiente situación. Se ha empleado el método símplex para obtener una solución óptima para un problema de programación lineal con valores específicos para los parámetros bi, cj y aij. Para iniciar el análisis de sensibilidad se cambian uno o más parámetros. Después de hacer los cambios, sean bi, cj y aij los valores de los parámetros; en notación matricial:
El primer paso es actualizar la tabla símplex final para que refleje estos cambios. Si se sigue usando la notación presentada en la tabla 5.9, al igual que las fórmulas que la acompañan para la idea fundamental [ 1) t* = t + y*T y 2)T* = S*T], la tabla símplex final revisada se calcula a partir de y* y S* (que no ha cambiado) y la nueva tabla inicial, tal y como se muestra en la tabla 6.17.
b → b c→c, A→A.
El primer paso es actualizar la tabla símplex final para que refleje estos cambios. Si se sigue usando la notación presentada en la tabla 5.9, al igual que las fórmulas que la acompañan para la idea fundamental [ 1) t* = t + y*T y 2)T* = S*T], la tabla símplex final revisada se calcula a partir de y* y S* (que no ha cambiado) y la nueva tabla inicial, tal y como se muestra en la tabla 6.17.
lunes, 24 de marzo de 2014
Esencia del análisis de sensibilidad (II)
Por estas razones es importante llevar a cabo un análisis de sensibilidad, para investigar el efecto que tendía sobre la solución óptima proporcionada por el método símplex el hecho de que los parámetros tomaran otros valores posibles. En general, habrá algunos parámetros a los que se les pueda asignar cualquier valro razonable sin que afecten la optimalidad de esta solución. Sin embargo, también habrá parámetros con valores probables que lleven a una nueva solución óptima. Esta situación es particularmente seria, si la solución original adquiere valores sustancialmente inferiores en la función objetivo, o tal vez no factibles! Por tanto, el objetivo fundamental del análisis de sensibilidad es identificar estos parámetros sensibles, para que se ponga una atención especial en su estimación y para seleccionar una solución cuyo desempeño sea bueno para la mayor parte de sus valores probables.
El análisis de sensiblidad requeriría un esfuerzo computacional exorbitante si fiera necesario volver a aplicar el método símplex desde el principio para investigar cada cambio en el valor de un parámetro. Por fortuna, la idea fundamental presentada en la sección 5.3 prácticamente elimina el esfuerzo computacional. En esencia, la idea fundamental revela de inmediato la forma en que los cambios en el modelo original alterarían los números de la tabla símplex final (si se supone que se duplica la misma secuencia de operaciones algebraicas que realizó el método símplex la primera vez). Entonces, después de hacer unso cuantos cálculos para actualizar esta tabla, se puede verificar con facilidad si la solución básica factible óptima original ahora es no óptima (o no factible). Si es así, esta solución se usará como solución básica inicial para comenzar de nuevo el símplex (o el dual símplex) para encontrar una nueva solución óptima, si se desea. Si los cambios en el modelo no son cambios mayores, sólo se requerirán unas cuantas iteraciones para obtener la nueva solución óptima a partir de esta solución básica inicial "avanzada".
domingo, 23 de marzo de 2014
Esencia del análisis de sensibilidad (I)
El trabajo del equipo de investigación de operaciones apenas comienza cuando se ha aplicado con éxito el método símplex para identificar una solución óptima del modelo. Como se dijo al final de la sección 3.3, una suposición de programación lineal es que todos los parámetros del modelo (las aij, bi y cj) son constantes conocidas. En realidad, los valores de los parámetros que se usan en el modelo casi siempre son sólo estimaciones basadas en una predicción de las condiciones futuras. Los datos obtenidos para desarrollar estas estimaciones con frecuencias son bastante imperfectos o no existen, así que los parámetros de formulación original pueden representar un poco más que algunas reglas cortas proporcionadas por el personal de línea al que tal vez se presionó para dar su opinión. Pueden incluso representar estimaciones optimistas o pesimistas que protegen los intereses de los estimadores.
Por todo esto, un gerente razonable y el personal de investigación de operaciones mantendrán una cierta duda saludable respecto a los números que salen de la computadora y, en muchos casos, los tomarán como un punto de partida para el análisis posterior del problema. Una solución "óptima" es óptima nada más en lo que se refiere al modelo especificó que se está usando para representar el problema real, y tal solución no se convierte en una guía confiable para la acción hasta que se verifica que su comportamiento es bueno también para otras representaciones razonables del problema. Más todavía, algunas veces los parámetros del modelo (en particular las bi) se establecen como resultado de decisiones por políticas gerenciales (por ejemplo, la cantidad de recursos que se asignan a las actividades), y estas decisiones deben revisarse después de ver sus consecuencias potenciales.
sábado, 22 de marzo de 2014
Otras aplicaciones (II)
Cuando se investigan los efectos de los cambios en las bi o en las aij (para las variables básicas), la solución óptima original puede convertirse en una solución superóptima (véase la tabla 6.10). Si se desea reoptimizar para identificar la nueva solución óptima, se debe aplicar el método dual símplex (presentado al final de las secciones 6.1 y 6.3), y comenzar con esta solución.
En la sección 6.1 se mencionó que a veces es más eficiente resolver el problema dual mediante el método símplex con el fin de identificar una solución óptima para el problema primal. Cuando la solución se encuentra de esta manera, el análisis de sensibilidad para el problema primal se lleva a cabo aplicandoel procedimiento que se describe en las dos secciones siguientes directamente al problema dual y después infiriendo los efectos complementarios sobre el problema primal (por ejemplo, véase la tabla 6.11). Este enfoque al análisis de sensibilidad es casi directo gracias a las estrechas relaciones primal-dual descritas en las secciones 6.1 y 6.3.
En la sección 6.1 se mencionó que a veces es más eficiente resolver el problema dual mediante el método símplex con el fin de identificar una solución óptima para el problema primal. Cuando la solución se encuentra de esta manera, el análisis de sensibilidad para el problema primal se lleva a cabo aplicandoel procedimiento que se describe en las dos secciones siguientes directamente al problema dual y después infiriendo los efectos complementarios sobre el problema primal (por ejemplo, véase la tabla 6.11). Este enfoque al análisis de sensibilidad es casi directo gracias a las estrechas relaciones primal-dual descritas en las secciones 6.1 y 6.3.
viernes, 21 de marzo de 2014
Otras aplicaciones (I)
Se han presentado ya otras dos aplicaciones importantes de la teoría de dualidad al analísis de sensibilidad, a saber, los precios sombra y el método dual símplex. Como se describió en las secciones 4.7 y 6.2, la solución óptima dual (y1*, y2*,......ym*) proporciona los precios sombra para los recursos respectivos que indican cuánto puede cambiar Z si se hicieran cambios (pequeños) en las bi (la cantidad de recursos). El análisis que resulta se ilustrará con algún detalle en la sección 6.7.
En términos más generales, la interpretación económica del problema dual y del método símplex que se presentó en la sección 6.2 proporciona algunas ideas útiles para el análisis de sensibilidad.
jueves, 20 de marzo de 2014
Introducción de una nueva variable (III)
Para responder esta pregunta se verifica la solución básica complementaria para el problema dual, que la tabla 6.9 se identifica como
Puesto que esta solución era óptima para el problema dual original, sin duda satisface las restricciones duales originales que se muestran en la tabla 6.1. Pero, satisface la nueva restricción dua,
Al sustituir esta solución.
se satisface, por lo que esta solución dual sigue siendo factible (es decir, óptima). En consecuencia, la solución primal original (2,6,2,0,0) junto con xnueva = 0 todavía es óptima y se concluye que no debe incluirse este nuevo producto en la producción.
Este enfoque hace que también sea muy sencillo llevar a cabo un análisis de sensibilidad sobre los coeficientes de la nueva variable que se agregó al problema original. Con sólo verificar la nueva restricción dual se puede saber de inmediato cuánto se pueden cambiar los valores de estos parámetros antes de que afecten la factibilidad de la solución dual, y por tanto, la optimalidad de la solución primal.
(y1, y2, y3,z1-c1, z2-c2) = (0, 3/2, 1, 0, 0)
Puesto que esta solución era óptima para el problema dual original, sin duda satisface las restricciones duales originales que se muestran en la tabla 6.1. Pero, satisface la nueva restricción dua,
2y1 + 3y2 +y3 ≥ 4?
Al sustituir esta solución.
2(0) + 3(3/2) + (1) ≥ 4
se satisface, por lo que esta solución dual sigue siendo factible (es decir, óptima). En consecuencia, la solución primal original (2,6,2,0,0) junto con xnueva = 0 todavía es óptima y se concluye que no debe incluirse este nuevo producto en la producción.
Este enfoque hace que también sea muy sencillo llevar a cabo un análisis de sensibilidad sobre los coeficientes de la nueva variable que se agregó al problema original. Con sólo verificar la nueva restricción dual se puede saber de inmediato cuánto se pueden cambiar los valores de estos parámetros antes de que afecten la factibilidad de la solución dual, y por tanto, la optimalidad de la solución primal.
miércoles, 19 de marzo de 2014
Introducción de una nueva variable (II)
Para ver un ejemplo, supóngase que en el problema de la Wyndor Glass Co. de la sección 3.1 se planea incluir en la línea de producción un tercer producto nuevo. Si xnueva representa la tasa de producción de este artículo, el modelo revisado que resulta es:
Después de introducir las variables de holgura, la solución óptima original par este problema sin xnueva era (x1, x2,x3,x4, x5) = (2,6,2,0,0), Si se incluye xnueva = 0 es todavia óptima la solución?
Después de introducir las variables de holgura, la solución óptima original par este problema sin xnueva era (x1, x2,x3,x4, x5) = (2,6,2,0,0), Si se incluye xnueva = 0 es todavia óptima la solución?
martes, 18 de marzo de 2014
Introducción de una nueva variable (I)
Como se indico en la tabla 6.6, las variables de decisión del modelo suelen representar el nivel de la distintas actividades bajo consideración. En algunas situaciones, estas actividades se seleccionan entre un grupo grande de actividades posibles en el que las actividades restantes no se eligieron por parecer menos atractivos. O quizá estas otras actividades no salieron a relucir hasta después de formular y resolver el modelo original. De cualquier manera, la pregunta en este caso es si alguna de estas actividades no consideradas antes valen la pena como para justificar su inclusión. En otras palabras, cambiará la solución óptima original si se agrega cualquiera de estas actividades?
Agregar otra actividad equivale a introducir en el modelo una nueva variable, con los coeficientes apropiados en las restricciones funcionales y en la función objetivo. El único cambio que resulta en el problema dual es la introducción de una nueva restricción.
Una vez hechos estos cambios, será la solución óptima original, junto con la nueva variable igual a cero (no básica), todavía óptima para el problema primal? Igual que en el caso anterior, una pregunta equivalente es si todavía es factible la solución básica complementaria para el problema dual, e igual que antes, esta pregunta se puede contestar con sólo verificar si esta solución básica complementaria satisface una restricción, que en este caso es la nueva restricción para el problema dual.
lunes, 17 de marzo de 2014
Cambios en los coeficientes de una variable no básica
Supóngase que los cambios que se hacen en el modelo original ocurren en los coeficientes de una variable que era no básica en la solución óptima original. Cuál es el efecto de estos cambios sobre esta solución? Es todavía factible? Es todavía óptima?
En vista de que la variable en cuestión es no básica (vale cero), el cambio en sus coeficientes no puede afectar la factibilidad de la solución, por lo cual, la pregunta que queda abierta en este caso es si todavía es óptima. Como se indica en las tablas 6.10 y 6.11, una pregunta equivalente es si la solución básica complementaria para el problema dual todavía es factible después de hacer estos cambios. Como estos cambios afectan al problema dual nada más en una restricción, la pregunta se puede responder al verificar si esta solución básica complementaria satisface esta restricción revisada.
Se ilustrará este caso es la subsección correspondiente de la sección 6.7 después de desarrollar el ejemplo adecuado.
En vista de que la variable en cuestión es no básica (vale cero), el cambio en sus coeficientes no puede afectar la factibilidad de la solución, por lo cual, la pregunta que queda abierta en este caso es si todavía es óptima. Como se indica en las tablas 6.10 y 6.11, una pregunta equivalente es si la solución básica complementaria para el problema dual todavía es factible después de hacer estos cambios. Como estos cambios afectan al problema dual nada más en una restricción, la pregunta se puede responder al verificar si esta solución básica complementaria satisface esta restricción revisada.
Se ilustrará este caso es la subsección correspondiente de la sección 6.7 después de desarrollar el ejemplo adecuado.
domingo, 16 de marzo de 2014
Papel de la teoría de dualidad en el análisis de sensibilidad
Como se describirá en las siguientes dos secciones, el análisis de sensibilidad consiste principalmente en la investigación del efecto que tiene sobre la solución óptima, el hecho de hacer cambios en los variables de los parámetros del modelo (aij, bi y cj). Sin embargo, los cambios de parámetros en el problema primal hacen que también cambien los valores correspondientes en el problema dual. Por tanto, se puede elegir qué problema se va a usar para investigar los cambios. GRacias a las relaciones primal-dual presentadas en las secciones 6.1 y 6.3 (en especial la propiedad de soluciones básicas complementarias), es fácil ir de un problema a otro según se quiera. En algunos casos es más conveniente analizar el problema dual directamente con objeto de determinar el efecto complementario sobre el problema primal. Se comenzará por considerar los casos.
sábado, 15 de marzo de 2014
Adaptación a otras formas del primal (VII)
El coeficiente de xj^-, a saber (zj^-cj) se debe ignorar. Salvo en estos casos, los coeficientes del renglón 0 se usan como antes (véase la sección 6.3) para obtener los valores de las variables duales correspondientes.
Para ilustrar este procedimiento se pide al lector que consulte el conjunto de tablas símplex dadas en la tabla 4.12 para el ejemplo de terapia de radiación. Las primeras tres tablas símplex contienen todavía variables artificiales como variables básicas, pero éste no es el caso en la tabla final, así que se puede usar su renglón 0 para identificar la solución óptima del problema dual que se muestra en la tabla 6.16. La primera restricción primal es una restricción estándar, por lo que y1 es justo el coeficiente de la primera variable de holgura (x3), o y1= 0.5. La segunda restricción es de igualdad, así que se observa el coeficiente de su variable artificial (x4) para obtener
La tercera restricción tiene el lado derecho negativo, por lo que se usa el coeficiente de su variable de holgura (x5) para obtener y3 = 0. Como antes, las variables de superávit para el problema dual son los coeficientes de las variables originales, x1 y x2, con lo que (z1 - c1) = 0, (z2-c2) = 0. Esto completa la solución básica dual óptima,
Para ilustrar este procedimiento se pide al lector que consulte el conjunto de tablas símplex dadas en la tabla 4.12 para el ejemplo de terapia de radiación. Las primeras tres tablas símplex contienen todavía variables artificiales como variables básicas, pero éste no es el caso en la tabla final, así que se puede usar su renglón 0 para identificar la solución óptima del problema dual que se muestra en la tabla 6.16. La primera restricción primal es una restricción estándar, por lo que y1 es justo el coeficiente de la primera variable de holgura (x3), o y1= 0.5. La segunda restricción es de igualdad, así que se observa el coeficiente de su variable artificial (x4) para obtener
y'2 = ( M-1.1) - M = -1.1.
La tercera restricción tiene el lado derecho negativo, por lo que se usa el coeficiente de su variable de holgura (x5) para obtener y3 = 0. Como antes, las variables de superávit para el problema dual son los coeficientes de las variables originales, x1 y x2, con lo que (z1 - c1) = 0, (z2-c2) = 0. Esto completa la solución básica dual óptima,
(y1, y'2, y3, Z1 - c1, z2 - c2) = (0.5, -1.1, 0, 0, 0)
viernes, 14 de marzo de 2014
Adaptación a otras formas del primal (VI)
Cuando se aplica el método símplex a formas primales no estándar y cuando se usa la técnica de variables artificiales (quizá con la ayuda del método de la M) para adaptarse a ellas, también debe hacerse algún ajuste a la interpretación de dualidad del renglón 0. Esto se debe a que las variables artificiales y las cantidades M revisan el problema primal y, por lo tanto, el problema dual cambia y las soluciones básicas complementarias que se muestran en el renglón 0 son soluciones de este problema dual revisado. Sin embargo, una vez que se han elminado las variables artificiales (se han hecho no básicas) y que la solución actual es una solución básica factible legítima para el problema primal original, se puede usar el renglón 0 para identificar la solución básica complementaria para el problema dual original. En seguida se describirá cómo se hace esto.
Supóngase que se usa la forma de la primera columna de la tabla 6.14. Para cada restricción de igualdad i, su variable artificial juega el papel de variable de holgura, excepto que al principio se agrego M al coeficiente de esta variable en el renglón 0. Por tanto, el valor actual de al variable dual correspondiente yi, es el coeficiente actual de esta variable artificial menos M. Su una restricción del tipo ≤ tiene lado derecho negativo desde el inicio (tal vez era una restricción ≥ y se cambió), de manera que se le ha agregado una variable artificial, el valor de la variable dual correspondiente sigue siendo el coeficiente de su variable de holgura. En este caso se ignora el coeficiente de la variable artificial. Por último, si la variable x es no restringirla en signo y se ha sustituido por la diferencia de dos variables no negativas (xj^+ - xj^-), el coeficiente de xj^+, denotado por (zj^+ - cj), se usará como si se tratara de xj. En otras palabras,
Supóngase que se usa la forma de la primera columna de la tabla 6.14. Para cada restricción de igualdad i, su variable artificial juega el papel de variable de holgura, excepto que al principio se agrego M al coeficiente de esta variable en el renglón 0. Por tanto, el valor actual de al variable dual correspondiente yi, es el coeficiente actual de esta variable artificial menos M. Su una restricción del tipo ≤ tiene lado derecho negativo desde el inicio (tal vez era una restricción ≥ y se cambió), de manera que se le ha agregado una variable artificial, el valor de la variable dual correspondiente sigue siendo el coeficiente de su variable de holgura. En este caso se ignora el coeficiente de la variable artificial. Por último, si la variable x es no restringirla en signo y se ha sustituido por la diferencia de dos variables no negativas (xj^+ - xj^-), el coeficiente de xj^+, denotado por (zj^+ - cj), se usará como si se tratara de xj. En otras palabras,
jueves, 13 de marzo de 2014
Adaptación a otras formas del primal (V)
De manera equivalente, se puede usar la forma en la primera columna de la tabla 6.14 en lugar de establecer el problema primal (Esta forma se necesita de todas maneras para aplicar el método símplex como se presentó en el capítulo 4.) Empleando las primeras dos conversiones en la tabla 6.12, este enfoque conduce a la forma del problema primal que se muestra en el lado izquierdo de la tabla 6.16. Entonces se usa la forma dual correspondiente en la segunda columna de la tabla 6.14 para construir el problema dual que se muestra en el lado derecho de la tabla 6.16.
Nótese que las dos versiones de los problemas primal y dual en las tablas 6.15 y 6.16 son completamente equivalentes, donde y'2 = -y2. Esta equivalencia es inevitable puesto que las diferencias implican que se sustituyen sólo formas equivalentes.
Nótese que las dos versiones de los problemas primal y dual en las tablas 6.15 y 6.16 son completamente equivalentes, donde y'2 = -y2. Esta equivalencia es inevitable puesto que las diferencias implican que se sustituyen sólo formas equivalentes.
miércoles, 12 de marzo de 2014
Adaptación a otras formas del primal (IV)
Para ilustrar este procedimiento, considérese el ejemplo de terapia de radiación que se presentó en la sección 3.4. (Su modelo se muestra en la página 45). Sea éste el problema primal. Antes de encontrar su problema dual, es necesario convertir el modelo en una de las formas permitidas que se muestran en la tabla 6.14. Se hará de las dos maneras.
El modelo de terapia de radiacion casi se ajusta a la forma en la segunda columna de la tabla 6.14. la única discrepancia es que la primera restricción funcional, 0.3x1 + 0.1x2 ≤ 27, se encuentra en la forma ≤ en lugar de ≥ 0 =. Sin embargo, si se multiplican ambos lados por (-1), se convierte a la forma ≥, quedando así la forma permitida del modelo que se muestra en el lado izquierdo de la tabla 6.15. Su problema dual se construye entonces en forma normal (según se resumió en la tabla 6.2a) excepto por la siguiente forma en la primera columna de la tabla 6.14. El resultado se muestra en el lado derecho de la tabla 6.15. Nótese que se ha eliminado la restricción de no negatividad para la segunda variable (y2) ya que la segunda restricción funcional en el problema primal es una restricción de igualdad.
El modelo de terapia de radiacion casi se ajusta a la forma en la segunda columna de la tabla 6.14. la única discrepancia es que la primera restricción funcional, 0.3x1 + 0.1x2 ≤ 27, se encuentra en la forma ≤ en lugar de ≥ 0 =. Sin embargo, si se multiplican ambos lados por (-1), se convierte a la forma ≥, quedando así la forma permitida del modelo que se muestra en el lado izquierdo de la tabla 6.15. Su problema dual se construye entonces en forma normal (según se resumió en la tabla 6.2a) excepto por la siguiente forma en la primera columna de la tabla 6.14. El resultado se muestra en el lado derecho de la tabla 6.15. Nótese que se ha eliminado la restricción de no negatividad para la segunda variable (y2) ya que la segunda restricción funcional en el problema primal es una restricción de igualdad.
martes, 11 de marzo de 2014
Adaptación a otras formas del primal (III)
La ejemplificación de la construcción del problema dual para un problema primal no estándar no incluyó restricciones de igualdad ni variables no restringidas en signo. De hecho, para estas dos formas existe un camino más corto. ES posible demostrar [véanse los problemas 20 y 17c)] que una restricción de igualdad en el primal debe manejarse como igual que una de la forma ≤ al construir el problema dual, excepto que debe eliminarse la restricción de no negatividad para la variable dual correspondiente (es decir, esta variable queda sin restricción de signo). Por la propiedad de simétria, eliminar una restricción de no negatividad en el problema primal afecta el problema dual sólo en que la restricción correspondiente cambia a una restricción de igualdad.
Gracias a estos atajos, sólo se necesita cambiar el problema primal a la forma que se muestra en cualquiera de las dos columnas de la tabla 6.14. Después se construye el problema dual de la manera acostumbrada y se emplea la forma que se muestra en la otra columna. Las flechas de dos sentidos en la tabla 6.14 muestran la correspondencia específica que debe seguirse entre las dos formas. En particular, una restricción funcional en forma de desigualdad en un problema corresponde a incluir una restricción de no negatividad en el otro, mientras que una restricción en forma de igualdad en un problema corresponde a quitar la restricción de no negatividad en el otro. Debe tenerse cuidado de no mezclar el problema primal. Las mezclas de este tipo no se permiten cuando se trata de construir el problema dual.
Gracias a estos atajos, sólo se necesita cambiar el problema primal a la forma que se muestra en cualquiera de las dos columnas de la tabla 6.14. Después se construye el problema dual de la manera acostumbrada y se emplea la forma que se muestra en la otra columna. Las flechas de dos sentidos en la tabla 6.14 muestran la correspondencia específica que debe seguirse entre las dos formas. En particular, una restricción funcional en forma de desigualdad en un problema corresponde a incluir una restricción de no negatividad en el otro, mientras que una restricción en forma de igualdad en un problema corresponde a quitar la restricción de no negatividad en el otro. Debe tenerse cuidado de no mezclar el problema primal. Las mezclas de este tipo no se permiten cuando se trata de construir el problema dual.
lunes, 10 de marzo de 2014
Adaptación a otras formas del primal (II)
Como resultado, todas las afirmaciones que se hicieron antes sobre las relaciones del problema dual con el primal también se cumplen en el sentido inverso.
Otra consecuencia de la propiedad de simetría es que no tiene ninguna trascendencia a cuál de los problemas se le dé el nombre de primal y a cuál el de dual. En la práctica, se puede encontrar un problema de programación lineal que se ajuste a nuestra forma estándar y al que se le dé de problema dual. La convención es que el modelo formulado para representar el problema real recibe el nombre de problema primal sin importar qué forma tiene.
Otra consecuencia de la propiedad de simetría es que no tiene ninguna trascendencia a cuál de los problemas se le dé el nombre de primal y a cuál el de dual. En la práctica, se puede encontrar un problema de programación lineal que se ajuste a nuestra forma estándar y al que se le dé de problema dual. La convención es que el modelo formulado para representar el problema real recibe el nombre de problema primal sin importar qué forma tiene.
domingo, 9 de marzo de 2014
Adaptación a otras formas del primal (I)
Hasta este momento se ha supuesto que el modelo del problema primal se encuentra en nuestra forma estándar. Sin embargo, al principio del capítulo se dijo que cualquier problema de programación lineal, en forma estándar o no, posee un problema dual. En esta sección se enfocará la atención a los cambios que sufre el dual para las otras formas del primal.
En la sección 4.6 se presentaron las otras formas no estándar, y se señalo cómo puede convertirse cada una en la forma estándar equivalente, si así se desea. Estas conversiones se resumen en la tabla 6.12. Con esto, siempre se tiene la opción de convertir cualquier modelo a nuestra forma estándar y después construir su problema dual en la forma usual. Como ejemplo, en la tabla 6.13 se hace esto para el problema dual estándar (que también debe tener un dual). Notese que el resultado de todo esto es justo el problema primal estándar! Como cualquier par de problemas primal y dual se pueden cambiar a estas formas, este hecho demuestra una propiedad importante de las relaciones primal-dual:
En la sección 4.6 se presentaron las otras formas no estándar, y se señalo cómo puede convertirse cada una en la forma estándar equivalente, si así se desea. Estas conversiones se resumen en la tabla 6.12. Con esto, siempre se tiene la opción de convertir cualquier modelo a nuestra forma estándar y después construir su problema dual en la forma usual. Como ejemplo, en la tabla 6.13 se hace esto para el problema dual estándar (que también debe tener un dual). Notese que el resultado de todo esto es justo el problema primal estándar! Como cualquier par de problemas primal y dual se pueden cambiar a estas formas, este hecho demuestra una propiedad importante de las relaciones primal-dual:
Propiedades de simetría
Para cualquier problema primal y su problema dual, todas las relaciones entre ellos deben ser simétricas ya que el dual de este problema dual es este problema primal.sábado, 8 de marzo de 2014
Ejemplo Soluciones básicas complementarias (IV)
Usando estas definiciones, en la tabla 6.11 se resumen las relaciones generales entre las soluciones básicas complementarias. En la figura 6.1 se muestra el rango de valores posible (comunes) para las funciones objetivo (Z=yo) que resulta para los tres pares de soluciones dados en la tabla 6.11 (el último par puede tener cualquier valor). Entonces, mientras que el método símplex maneja directamente soluciones básicas subóptimas y trabaja para alcanzar la optimalidad en el problema primal, al mismo tiempo obtiene de manera indirecta las soluciones superóptimas complementarias y las mueve hacia la factibilidad del problema dual. A la inversa, algunas veces es más conveniente (o necesario) trabajar directamente con las soluciones básicas subóptimas y trabajar para alcanzar la optimalidad en el problema primal, lo cual es el propósito del método símplex descrito en la sección 9.2.
Se ha comprobado la utilidad de estas relaciones, en particular para el análisis de sensibilidad, como se verá más adelante en el capítulo.
Se ha comprobado la utilidad de estas relaciones, en particular para el análisis de sensibilidad, como se verá más adelante en el capítulo.
viernes, 7 de marzo de 2014
Ejemplo Soluciones básicas complementarias (III)
Para revisar el razonamiento que fundamenta esta propiedad, obsérvese que la solución dual (y*, z* - c) debe ser factible para el problema dual, puesto que la condición de optimalidad para el problema primal requiere que todas estas variables duales (inclusive las variables de superávit) sean no negativas. Como esta solución es factible, debe ser óptima para el problema dual dada a la propiedad de dualidad débil.
Las soluciones básicas se pueden clasificar según si satisfacen o no cada una de dos condiciones. Una es la condición de factibilidad, a saber, si todas las variables (incluyendo las de holgura) en la solución aumentanda son no negativas. La otra es la condición de optimalidad, es decir, si todos los coeficientes en el renglón 0 (o sea todas la variables en la solución básica complementaria) son no negativos. En la tabla 6.10 se resumen los términos que se emplean aquí para los diferentes tipos de soluciones básicas. Por ejemplo, en la tabla 6.9 las soluciones básicas 1,2,4 y 5 son subóptimas, la 6 es óptima, la 7 y 8 son superóptimas y la 3 no es ni factible ni superóptima.
jueves, 6 de marzo de 2014
Propiedad de las soluciones básicas óptimas complementarias
Cada solución básica óptima en el problema primal tiene una solución básica óptima complementaria en el problema dual, en donde los valores respectivos de las funciones objetivo (Z y yo) son iguales. Dado el renglón 0 de la tabla símplex para la solución primal óptima, se puede encontrar la solución dual óptima complementaria (y*, Z*-c), como se puede ver en la tabla 6.4.
miércoles, 5 de marzo de 2014
Relaciones entre las soluciones básicas complementarias
Ahora se estudiarán las relaciones entre las soluciones básicas complementarias y se comenzará con sus relaciones de factibilidad. Las columnas centrales de la tabla 6.9 proporcionan algunas ideas valiosas. Nótese que para los pares de soluciones básicas complementarias, las respuestas de sí o no a la factibilidad también satisfacen una relación de complementariedad en la mayor parte de los casos. En particular, con una sola excepción, siempre que una solución es factible, la otra no lo es. (También es posible que ninguna solución sea factible, como ocurre con el tercer par). La única excepción es el sexto par, en el que se sabe que la solución del primal es óptima. La columna Z = yo sugiere la explicación. Como la sexta solución dual también es óptima (por la propiedad de soluciones óptimas complementarias), con yo = 36, entonces las primeras cinco soluciones duales no pueden ser factibles, ya que yo < 36, entonces las primeras cinco soluciones duales no pueden ser factibles, ya que yo < 36 (recuérdese que el objetivo del problema dual es minimizar yo). Por la misma razón, las dos últimas soluciones primales no pueden ser factibles, pues Z > 36.
Esta explicación está apoyada por la propiedad de dualidad fuerte que dice que las soluciones óptimas primal y dual tienen Z = yo.
En seguida se establecerá la extensión de la propiedad de las soluciones óptimas complementarias de la sección 6.1 para las formas aumentadas de los dos problemas.
Esta explicación está apoyada por la propiedad de dualidad fuerte que dice que las soluciones óptimas primal y dual tienen Z = yo.
En seguida se establecerá la extensión de la propiedad de las soluciones óptimas complementarias de la sección 6.1 para las formas aumentadas de los dos problemas.
martes, 4 de marzo de 2014
Ejemplo Soluciones básicas complementarias (II)
En forma alternativa, para cada solución básica primal se puede usar la propiedad de holgura complementaria para identificar las variables básicas y no básicas de la solución básica dual complementaria, de manera que el sistema de ecuaciones dado al principio de la sección se puede resolver directamente para obtener esta solución complementaria. Por ejemplo, considérese la penúltima solución básica primal en la tabla 6.9, en donde x1, x2 y x5 son variables básicas. En las tablas 6.7 y 6.8 se observa que la propiedad de holgura complementaria implica que (z1-c1), (z2-c2) y y3 son variables no básicas en la solución básica dual complementaria. Al establecer estas variables igual a cero en las ecuaciones del problema dual, y1 + 3y3 - (z1-c1) = 3 y 2y2 + 2y3 -(z2-c2) =5, de inmediato se obtiene y1 = 3, y2 = (5/2).
Por último, obsérvese que la tabla 6.9 demuestra que (0, 3/2, 1, 0, 0) es la solución óptima para el problema dual, ya que es la solución básica factible con un valor mínimo para yo (36).
lunes, 3 de marzo de 2014
Ejemplo Soluciones básicas complementarias (I)
Para ilustrar estas dos propiedades, considérese de nuevo el problema de la Wyndor Glass Co. de la sección 3.1. En las tablas 5.5 y 5.6 se muestran sus ocho soluciones básicas (cinco factibles y tres no factibles) junto con las respectivas soluciones en los vértices. Entonces, su problema dual (veáse la tabla 6.1) también debe tener ocho soluciones básicas, cada una complementaria a una de las soluciones primales, como se muestra en la tabla 6.9.
Las tres soluciones básicas factibles obtenidas por el método símplex para el problema primal son la primera, la quinta y la sexta soluciones que se muestran en la tabla 6.9. Ya se vio en la tabla 6.5 cómo se pueden leer las soluciones básicas complementarias para el problema dual directamente del renglón 0, se comienza con los coeficientes de las variables de holgura y se sigue con las variables originales. Las otras soluciones básicas duales también se pueden identificar en la misma forma si se construye el renglón 0 para cada una de las otras soluciones básicas primales, empleando las fórmulas dadas en la parte inferior de la tabla 5.7.
Las tres soluciones básicas factibles obtenidas por el método símplex para el problema primal son la primera, la quinta y la sexta soluciones que se muestran en la tabla 6.9. Ya se vio en la tabla 6.5 cómo se pueden leer las soluciones básicas complementarias para el problema dual directamente del renglón 0, se comienza con los coeficientes de las variables de holgura y se sigue con las variables originales. Las otras soluciones básicas duales también se pueden identificar en la misma forma si se construye el renglón 0 para cada una de las otras soluciones básicas primales, empleando las fórmulas dadas en la parte inferior de la tabla 5.7.
domingo, 2 de marzo de 2014
Soluciones básicas complementarias (III)
La razón por la que se usa el nombre de holgura complementaria para esta última propiedad es que dice (en parte) que para cada par de variables asociadas, si una de ellas tiene holgura en su restricción de no negatividad (valor de la variable básica >0), entonces la otra no debe tener holgura (variable no básica = 0). En la sección 6.2 se mencionó que está propiedad tiene una interpretación económica útil en los problemas de programación líneal.
sábado, 1 de marzo de 2014
Propiedad de holgura complementaria
La siguiente propiedad indica cómo identificar las variables básicas y no básicas para esta solución básica complementaria.
Propiedad de holgura complementaria
Al usar la asociación entre variables que se da en la tabla 6.7, las variables en la solución básica primal y en la solución básica dual complementaria satisfacen las relaciones de holgura complementaria que se muestran en la tabla 6.8. Es más, esta relación es simétrica, de manera que estas dos soluciones básicas son complementarias entre sí.
Suscribirse a:
Entradas (Atom)