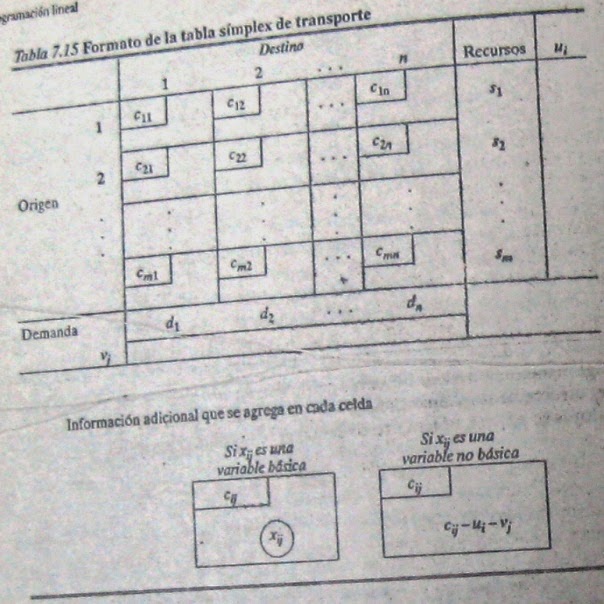
La gran conclusión es que se puede eliminar casi toda la tabla símplex (junto con todo el esfuerzo de actualizarla)! Además de los datos de entrada (los valores de cij, si y dj), la única información que necesita el método símplex de transporte es la solución básica factible actual, los valores actuales de ui y vj y los valores resultantes de (cij -ui - vj) para las variables xij no básicas. Cuando se resuelve un problema a mano es conveniente registrar esa información en una tabla símplex de transporte, como la que se muestra en la tabla 7.15. [Obsérvese con cuidado que los valores de xij y (cij - ui -vj) se distinguen en esta tabla encerrando en un círculo los primeros pero no estos últimos].
El lector podrá apreciar de manera global la gran diferencia en eficiencia y conveniencia entre los métodos símplex de transporte y símplex si aplica ambos al mismo problema pequeño (véase el problema 22). Sin embargo, la diferencia es más importante en problemas grandes que tienen que resolverse en una computadora. El tamaño de las tablas símplex y de transporte sugiere, de alguna manera, esta gran ganancia. Para un problema de transporte que tiene m orígenes y n destinos, la tabla símplex tiene (m+n+1) renglones y (m+1)(n+1) columnas (sin incluir las que se colocan a la izquierda de las columnas de xij), y la tabla símplex de transporte tendrá m renglones y n columnas (excluyendo los dos renglones y columnas de información adicional). Si se dan valores a m y n (por ejemplo, m = 10 y n =100, que sería un problema bastante normal de tamaño mediano), se puede observar cómo crece la razón del número de celdas en la tabla símplex entre el mismo número en la tabla de transporte, conforme m y n crecen.
sábado, 31 de mayo de 2014
viernes, 30 de mayo de 2014
Preparación para el método símplex (IV)
Segundo, el renglón 0 actual se puede obtener sin usar ningún otro renglón con sólo calcular los valores de ui y vj directamente. Como cada variable básica debe tener coeficiente cero en el renglón 0, estos valores se pueden obtener resolviendo el sistema de ecuaciones.
cij - ui - vj = 0 para cada i y j tal que xij es variable básica
lo cual se puede hacer de manera directa. (Nótese en la tabla 7.13 que la estructura especial hace posible esta forma conveniente de obtener el renglón 0 al dar como coeficientes de xij a cij - ui - vj en la tabla 7.14).
Tercero, la variable básica que sale se puede identificar de manera sencilla si usar (explícitamente) los coeficientes de la variable básica entrante. Esto también se debe a la estructura especial del problema, lo cual permite ver cómo debe cambiar la solución cuando crece el valor de la variable entrante. Como resultado, la nueva solución básica factible también se puede identificar de inmediato sin manipulaciones algebraicas sobre los renglones de la tabla símplex.
cij - ui - vj = 0 para cada i y j tal que xij es variable básica
lo cual se puede hacer de manera directa. (Nótese en la tabla 7.13 que la estructura especial hace posible esta forma conveniente de obtener el renglón 0 al dar como coeficientes de xij a cij - ui - vj en la tabla 7.14).
Tercero, la variable básica que sale se puede identificar de manera sencilla si usar (explícitamente) los coeficientes de la variable básica entrante. Esto también se debe a la estructura especial del problema, lo cual permite ver cómo debe cambiar la solución cuando crece el valor de la variable entrante. Como resultado, la nueva solución básica factible también se puede identificar de inmediato sin manipulaciones algebraicas sobre los renglones de la tabla símplex.
Etiquetas:
Problemas especiales de programación lineal
jueves, 29 de mayo de 2014
Preparación para el método símplex (III)
Con el fin de sentar las bases que permitan la simplificación, recuérdese cuál es la información que necesita el método símplex. En el paso inicial, debe obtenerse una solución básica factible inicial, lo que se hace en forma ficticia al introducir variables artificiales para que constituyan el conjunto de variables básicas iniciales cuyo valor es igual a las si y di. Para llevar a cabo la prueba de optimalidad y la parte 1 del paso iterativo (seleccionar una variable básica entrante) se requiere conocer el renglón 0, que se obtiene restando del renglón 0 anterior un cierto múltiplo de otro renglón. La parte 2 (determinar la variable básica que sale) debe identificar aquella variable básica que llega primero a cero cuando aumenta el valor de la variable básica entrante; esto se hace comparando los coeficientes actuales de la variable básica entrante con el lado derecho correspondiente. La parte 3 debe determinar la nueva solución básica factible, que se encuentra al restar cierto múltiplo de un renglón, de otros renglones de la tabla símplex actual.
La pregunta es cómo obtiene el método símplex de transporte la misma informació de una manera mucho más sencilla. La respuesta a esta pregunta es el tema de las páginas siguientes, pero se dará alguna información preliminar.
Primero, no se necesitan variables artificiales, pues se dispone de un procedimiento sencillo y conveniente (con algunas variaciones) para construir una solución inicial básica factible.
Etiquetas:
Problemas especiales de programación lineal
miércoles, 28 de mayo de 2014
Preparación para el método símplex (II)
Después de cualquier iteración subsecuente, el renglón 0 tendría la forma que se muestra en la tabla 7.14. A causa del patrón de ceros y unos que siguen los coeficientes en la tabla 7.13, la idea fundamental que se presentó en la sección 5.3 implica que ui y vj tienen la siguiente interpretación.
ui = múltiplo del renglón i original que se ha restado (directa o indirectamente) del renglón 0 original durante todas las iteraciones del método símplex que llevaron a la tabla actual.
vj = múltiplo del renglón (m+j) original que se ha restado (directa o indirectamente) del renglón 0 original durante todas las iteraciones del método símplex que llevaron a la tabla actual.
Si se toma en cuenta lo expuesto en el capítulo 6, se puede reconocer las ui y vj son las variables duales . Si xij es una variable no básica (cij - ui - vj) se interpreta como la tasa a la que Z cambiaría si se aumentara el valor de xij.
ui = múltiplo del renglón i original que se ha restado (directa o indirectamente) del renglón 0 original durante todas las iteraciones del método símplex que llevaron a la tabla actual.
vj = múltiplo del renglón (m+j) original que se ha restado (directa o indirectamente) del renglón 0 original durante todas las iteraciones del método símplex que llevaron a la tabla actual.
Si se toma en cuenta lo expuesto en el capítulo 6, se puede reconocer las ui y vj son las variables duales . Si xij es una variable no básica (cij - ui - vj) se interpreta como la tasa a la que Z cambiaría si se aumentara el valor de xij.
Etiquetas:
Problemas especiales de programación lineal
martes, 27 de mayo de 2014
Preparación para el método símplex (I)
Para hacer hincapié en la simplificación lograda por el método símplex de transporte, se revisará primero la forma en que el método símplex general (no simplificado) establecería el problema en la forma tabular. En la tabla 7.13 se muestra la forma que tendrían las columnas normales de la tabla símplex después de construir la tabla de restricciones (véase la tabla 7.6) , de convertir la función objetivo en la forma de maximización y de introducir las variables artificiales z1, z2,,,,,,, Zm+n con el método de la M, a los (m+n) restricciones de igualdad (véase la sección 4.6). En esta tabla, todos los elementos que no se muestran en estas columnas son ceros. [El único ajuste que queda por hacer antes de la primera iteración es el de eliminar algebraicamente los coeficientes distintos de cero de las variables básicas iniciales (artificiales) en el renglón 0.]
Etiquetas:
Problemas especiales de programación lineal
lunes, 26 de mayo de 2014
Método símplex simplificado para el problema de transporte
El problema de transporte es sólo un tipo especial de problemas de programación lineal y puede resolverse aplicando el método símplex tal y como se describió en el capitulo 4. Sin embargo en esta sección se verá que, si se aprovecha la estructura especial que se muestra en la tabla 7.6, se puede lograr un importante ahorro en los cálculos. Se hará referencia a este procedimiento simplificado como el método símplex de transporte.
Al avanzar en la lectura, obsérvese en particular la manera en que se aprovecha la estructura especial para lograr un menor esfuerzo computacional. Tengase presente que algunas veces se pueden lograr ahorros considerables si se aprovechan otras estructuras especiales, como las que se describirán más adelante.
Al avanzar en la lectura, obsérvese en particular la manera en que se aprovecha la estructura especial para lograr un menor esfuerzo computacional. Tengase presente que algunas veces se pueden lograr ahorros considerables si se aprovechan otras estructuras especiales, como las que se describirán más adelante.
Etiquetas:
Problemas especiales de programación lineal
domingo, 25 de mayo de 2014
Planteamiento Distribución de recursos hidráulicos (III)
La necesidad mínima de los Devils es igual a la cantidad solicitada, así que debe satisfacerse su demanda completa de 70 con agua de los orígenes reales y no del ficticio.
Esta restricción necesita la ayuda del método de la M! Si se asigna un costo muy alto de M a la asignación en la combinación del origen ficticio a Los Devils, se asegura que esta asignación sea cero en la solución óptima.
Por último, considérese Berdoo. A diferencia del caso de Hollyglass, los recursos del origen ficticio son suficientes para "abastecer" (en forma imaginaria) por lo menos parte de la necesidad mínima de Berdoo además de la cantidad adicional que solicita. Entonces, si la necesidad mínima es 30, se deben hacer ajustes para evitar que el origen ficticio contribuya en más de 20 al abastecimiento total (50) de Berdoo. Esto se logra si se divide Berdoo en do destinos, uno con 30 unidades de demanda y un costo M para cualquier asignación que provenga del origen ficticio, y la otra con una demanda de 20 y con costo unitario de cero para asignación del destino fícticio. Esta formulación lleva a la tabla de costos y requerimientos que se muestran en la tabla 7.12.
Este problema se resolverá en la siguiente sección para ilustrar el procedimiento de solución que se presenta ahí.
Esta restricción necesita la ayuda del método de la M! Si se asigna un costo muy alto de M a la asignación en la combinación del origen ficticio a Los Devils, se asegura que esta asignación sea cero en la solución óptima.
Por último, considérese Berdoo. A diferencia del caso de Hollyglass, los recursos del origen ficticio son suficientes para "abastecer" (en forma imaginaria) por lo menos parte de la necesidad mínima de Berdoo además de la cantidad adicional que solicita. Entonces, si la necesidad mínima es 30, se deben hacer ajustes para evitar que el origen ficticio contribuya en más de 20 al abastecimiento total (50) de Berdoo. Esto se logra si se divide Berdoo en do destinos, uno con 30 unidades de demanda y un costo M para cualquier asignación que provenga del origen ficticio, y la otra con una demanda de 20 y con costo unitario de cero para asignación del destino fícticio. Esta formulación lleva a la tabla de costos y requerimientos que se muestran en la tabla 7.12.
Este problema se resolverá en la siguiente sección para ilustrar el procedimiento de solución que se presenta ahí.
Etiquetas:
Problemas especiales de programación lineal
sábado, 24 de mayo de 2014
Planteamiento Distribución de recursos hidráulicos (II)
La situación es análoga al problema de programación de la producción de Northern Airplane en donde se tenía un exceso en la capacidad de abastecimiento, ahora se tiene un exceso en la capacidad de demanda. En consecuencia, en lugar de introducir un destino ficticio para que "reciba" los recursos que sobran, el ajuste será introducir un origen ficticio para "enviar" la capacidad de demanda no utilizada. La cantidad imaginaría de recursos para este origen ficticio corresponde al excedente de la suma de las demandas sobre la suma de los recursos reales:
(50 + 70 +30 +60 ) - (50 + 60 + 50) = 50
Este planteamiento conduce a una tabla de costos y requerimientos que se muestra en la tabla 7.11, en la que las unidades empleadas son millones de acres-pie y millones de dólares. Los costos en el renglón ficticio son cero por que las asignaciones ficticias no cuestan. Por otro lado, se asigna un costo alto, M, al elemento del Río Calorie a Hollyglass. La razón es que el agua del río Calorie no se puede usar para alimentar a la ciudad de Hollyglass y al asignar el costo M se evitará esta asignación.
Ahora se analizará cómo se pueden tomar en cuenta las necesidades mínimas de cada ciudad en este tipo de formulaciones. Como San Go no estableció para Hollyglass no requiere ajuste porque su demanda (60) excede (por 10) la cantidad disponible en el origen ficticio (50), con lo que la cantidad que le debe llegar desde los orígenes reales será por lo menos de 10 en cualquier solución factible y, por tanto, su necesidad mínima de 10 queda garantizada. (Si no hubiera ocurrido esta coincidencia, hubiera tenido que hacerse el mismo ajuste que se tiene que hacer para Berdoo)
(50 + 70 +30 +60 ) - (50 + 60 + 50) = 50
Este planteamiento conduce a una tabla de costos y requerimientos que se muestra en la tabla 7.11, en la que las unidades empleadas son millones de acres-pie y millones de dólares. Los costos en el renglón ficticio son cero por que las asignaciones ficticias no cuestan. Por otro lado, se asigna un costo alto, M, al elemento del Río Calorie a Hollyglass. La razón es que el agua del río Calorie no se puede usar para alimentar a la ciudad de Hollyglass y al asignar el costo M se evitará esta asignación.
Ahora se analizará cómo se pueden tomar en cuenta las necesidades mínimas de cada ciudad en este tipo de formulaciones. Como San Go no estableció para Hollyglass no requiere ajuste porque su demanda (60) excede (por 10) la cantidad disponible en el origen ficticio (50), con lo que la cantidad que le debe llegar desde los orígenes reales será por lo menos de 10 en cualquier solución factible y, por tanto, su necesidad mínima de 10 queda garantizada. (Si no hubiera ocurrido esta coincidencia, hubiera tenido que hacerse el mismo ajuste que se tiene que hacer para Berdoo)
Etiquetas:
Problemas especiales de programación lineal
viernes, 23 de mayo de 2014
Planteamiento Distribución de recursos hidráulicos (I)
La tabla 10.7 ya casi está en la forma apropiada de una tabla de costos y requerimientos, en donde los ríos son los orígenes y las ciudades, los destinos. La única dificultad básica es que no ha quedado claro cuáles deben ser las demandas en cada destino. De hecho, la cantidad que debe recibirse en cada una (excepto en Los Devils) es una variable de decisión con cotas superior e inferior. (La cota superior es la cantidad solicitada a menos que exceda la cantidad total disponible después de cumplir con las necesidades mínimas de las otras ciudades, en cuyo caso, esta cantidad disponible se convierte en la cota superior. La sedienta ciudad de Hollyglass tiene una cota superior de:
(50 + 60+ 50) - (30 +70 +0) = 60
Desafortunadamente, las cantidades de las demandas en la tabla de costos y requerimientos de un problema de transporte deben ser constantes, no variables de decisión acotadas. Para salvar esta dificultad, supóngase de momento que no es necesario satisfacer las necesidades mínimas con agua de estos ríos, de manera que las cotas superiores son las únicas restricciones sobre las cantidades que deben asignarse. En estas circunstancias, la pregunta es si las cantidades solicitadas pueden tomarse como la demanda en el planeamiento de un problema de transporte. La respuesta es sí.!, después de hacer un ajuste.
(50 + 60+ 50) - (30 +70 +0) = 60
Desafortunadamente, las cantidades de las demandas en la tabla de costos y requerimientos de un problema de transporte deben ser constantes, no variables de decisión acotadas. Para salvar esta dificultad, supóngase de momento que no es necesario satisfacer las necesidades mínimas con agua de estos ríos, de manera que las cotas superiores son las únicas restricciones sobre las cantidades que deben asignarse. En estas circunstancias, la pregunta es si las cantidades solicitadas pueden tomarse como la demanda en el planeamiento de un problema de transporte. La respuesta es sí.!, después de hacer un ajuste.
Etiquetas:
Problemas especiales de programación lineal
jueves, 22 de mayo de 2014
Ejemplo Distribución de recursos hidráulicos (II)
La administración del distrito tiene que resolver el problema de cómo asignar el agua disponible durante el próximo verano. En la columna del lado derecho de la tabla 7.10 se dan las cantidades disponibles en los tres rios, en unidades de un millón de acres-pie. El distrito se compromete a proporcionar una cantidad mínima para cumplir con las necesidades esenciales de cada ciudad (con la excepción de San Go, que tiene una fuente independiente de agua); estas necesidades mínimas se muestran en el renglón correspondiente en la tabla. El renglón de solicitado indica que Los Devils no quiere más agua que la que cubre sus necesidades mínimas, pero Berdo compraría hasta 20 más, San Go, hasta 30 más y Hollyglass compraría toda la que pudiera obtener.
La administración desea asignar toda el agua disponible de los tres ríos de manera que por lo menos se cumpla con las necesidades mínimas de cada ciudad y que al mismo tiempo se minimice el costo total.
Etiquetas:
Problemas especiales de programación lineal
miércoles, 21 de mayo de 2014
Ejemplo Distribución de recursos hidráulicos (I)
El distrito minero es una dependencia que administra la distribución de agua en una cierta región geográfica grande. La región es bastante árida, por lo que el distrito debe comprar y traer agua desde fuera de ella. Las fuentes de esta agua importada son los ríos Colombo, Sacron y Calorie. El distrito revende el agua a los usuarios de la región. Sus clientes principales son los departamentos de aguas de las ciudades de Berdoo, Los Devils, San Go y Hollyglass.
Es posible hacer llegar agua a cualquiera de estas ciudades desde cualquiera de los tres rios con excepción de que no hay forma de abastecer a Hollyglass con agua del río Calorie. Sin embargo, dada la distribución geográfica de los aceuductos y las ciudades en la región, lo que le cuesta al distrito el abastecimiento depende tanto de la fuente como de la ciudad a la que abastece. En la tabla 7.10 se dan los costos variables por acre-pie de agua (en dólares) para cada combinación de río y ciudad. A pesar de estas variaciones, el precio que el distrito cobra por acre-pie es independiente de la fuente de agua y es el mismo para todas las ciudades.
Es posible hacer llegar agua a cualquiera de estas ciudades desde cualquiera de los tres rios con excepción de que no hay forma de abastecer a Hollyglass con agua del río Calorie. Sin embargo, dada la distribución geográfica de los aceuductos y las ciudades en la región, lo que le cuesta al distrito el abastecimiento depende tanto de la fuente como de la ciudad a la que abastece. En la tabla 7.10 se dan los costos variables por acre-pie de agua (en dólares) para cada combinación de río y ciudad. A pesar de estas variaciones, el precio que el distrito cobra por acre-pie es independiente de la fuente de agua y es el mismo para todas las ciudades.
Etiquetas:
Problemas especiales de programación lineal
martes, 20 de mayo de 2014
Ejemplo de Programación de la Producción (VII)
Los costos asociados con el destino ficticio deben ser cero, ya que la asignación ficticia no significa costo alguno. (Los costos con valores M no sería apropiados para esta columna pues no se trata de forzar que los valores correspondientes de xij sean cero. De hecho, esos valores deben sumar 30.)
En la tabla 7.9 se proporciona la tabla final de costos y requerimientos en la que el destino ficticio se indica por 5(F)
Cuando se emplea esta formulación y el procedimiento de solución que se describe en la sección 7.2. (véase el problema 19 y su respuesta al final del blog), es bastante fácil encontrar el programa de producción óptimo.
En la tabla 7.9 se proporciona la tabla final de costos y requerimientos en la que el destino ficticio se indica por 5(F)
Cuando se emplea esta formulación y el procedimiento de solución que se describe en la sección 7.2. (véase el problema 19 y su respuesta al final del blog), es bastante fácil encontrar el programa de producción óptimo.
Etiquetas:
Problemas especiales de programación lineal
lunes, 19 de mayo de 2014
Ejemplo de Programación de la Producción (VI)
Para convertir las desigualdades en ecuaciones, se usa la familiar técnica de introducir variables de holgura, como se describió en la sección 4.2. En el contexto de este ejemplo, las variables de holgura se interpretan como asignaciones a un destino ficticio que representa la capacidad de producción no utilizada en el mes correspondiente. Este ajuste permite que el abastecimiento, en la formulación del problema de transporte, sea la capacidad de producción total en ese mes. Más aún , como la demanda en el destino ficticio es la capacidad total no utilizada, esta demanda es:
(25 + 35 + 30 +10) - (10 + 15 + 25+ 20) =30
Incluida esta demanda, la suma de los recursos ahora debe ser igual a la suma de las demandas, que es la condición dada por la propiedad de soluciones factibles para que existan soluciones factibles.
(25 + 35 + 30 +10) - (10 + 15 + 25+ 20) =30
Incluida esta demanda, la suma de los recursos ahora debe ser igual a la suma de las demandas, que es la condición dada por la propiedad de soluciones factibles para que existan soluciones factibles.
Etiquetas:
Problemas especiales de programación lineal
domingo, 18 de mayo de 2014
Ejemplo de Programación de la Producción (V)
Los números que necesitan insertarse en la columna de los recursos de la tabla 7.8 no son obvios, porque estos "recursos", es decir, las cantidades producidas en los meses respectivos, no son cantidades fijas. De hecho, el objetivo es encontrar los mejores valores para estas cantidades. De todas maneras, como ya se ha dicho, es necesario asignar un número fijo a todos los elementos de la tabla (también a los de la columna de recursos), para tener un problema de transporte. Aunque las restricciones sobre el abastecimiento no estén presentes en la forma usual, existen en forma de cotas superiores sobre la cantidad que se puede producir, a saber:
La única diferencia respecto al moldeo estándar para el problema d transporte es que estas restricciones están en forma de desigualdades en lugar de ecuaciones.
La única diferencia respecto al moldeo estándar para el problema d transporte es que estas restricciones están en forma de desigualdades en lugar de ecuaciones.
Etiquetas:
Problemas especiales de programación lineal
Ejemplo de Programación de la Producción (IV)
La tabla (incompleta) correspondiente, con los costos y requerimientos se da en la tabla 7.38
Lo que resta por hacer es identificar las cifras que faltan
Como es imposible producir motores en un mes determinado para instalarlos el mes anterior, xij debe ser cero para i > j. Por tanto, no hay un costo real que se pueda asociar a estas xij. De cualquier manera, con el fin de tener un problema de transporte bien definido al que se pueda aplicar un paquete de computadora estándar (procedimiento de solución de la sección 7.2) es necesario asignar algún valor a los costos no identificados. Por fortuna, se puede usar el método de la M introducido en la sección 2.4 para asignar este valor. Así, se asigna un número muy grande (que por conveniencia se denota por M) a estas cantidades no identificadas en la tabla de costos para reforzar a que los valores correspondientes de xij sean cero en la solución final.
Lo que resta por hacer es identificar las cifras que faltan
Como es imposible producir motores en un mes determinado para instalarlos el mes anterior, xij debe ser cero para i > j. Por tanto, no hay un costo real que se pueda asociar a estas xij. De cualquier manera, con el fin de tener un problema de transporte bien definido al que se pueda aplicar un paquete de computadora estándar (procedimiento de solución de la sección 7.2) es necesario asignar algún valor a los costos no identificados. Por fortuna, se puede usar el método de la M introducido en la sección 2.4 para asignar este valor. Así, se asigna un número muy grande (que por conveniencia se denota por M) a estas cantidades no identificadas en la tabla de costos para reforzar a que los valores correspondientes de xij sean cero en la solución final.
Etiquetas:
Problemas especiales de programación lineal
sábado, 17 de mayo de 2014
Ejemplo de Programación de la Producción (III)
Por otro lado, si se adopta un punto de vista diferente, sin duda se puede formular como un problema de transporte cuya solución requiere mucho menos esfuerzo. Este punto de vista diferente describirá el problema en términos de orígenes y destinos, y después identificará las xij, cij, si y dj correspondientes. (Trate el lector de hacerlo antes de leer lo que sigue)
Como las unidades que se van a distribuir son los motores de turbina, cada uno de los cuales debe programarse para un mes en particular e instalarse en un mes específico (tal vez distinto).
Origen i = producción de motores de turbina en el mes i (i = 1,2,3,4)
Destino j = instalación del motor de turbina en el mes j (j = 1,2,3,4)
xij = número de motores producidos en el mes i para instalarlos en el mes j
cij = costo asociado con cada unidad de xij
= {costo por unidad de producción y cualquier almacenaje, si i ≤ j?, si i < j
si = ?
dj = número de instalaciones programadas en el mes j.
Como las unidades que se van a distribuir son los motores de turbina, cada uno de los cuales debe programarse para un mes en particular e instalarse en un mes específico (tal vez distinto).
Origen i = producción de motores de turbina en el mes i (i = 1,2,3,4)
Destino j = instalación del motor de turbina en el mes j (j = 1,2,3,4)
xij = número de motores producidos en el mes i para instalarlos en el mes j
cij = costo asociado con cada unidad de xij
= {costo por unidad de producción y cualquier almacenaje, si i ≤ j?, si i < j
si = ?
dj = número de instalaciones programadas en el mes j.
Etiquetas:
Problemas especiales de programación lineal
jueves, 15 de mayo de 2014
Ejemplo de Programación de la Producción (II)
Dadas las variaciones en los costos de producción, podría valer la pena producir algunos motores un mes o dos antes de su fecha de instalación y se está estudiando esta posibilidad. El inconveniente es que esos motores deberán almacenarse hasta que sean instalados (la estructura de los aviones no estará lista antes). El costo de almacenaje para cada motor es de $15 000/mes (se incluye el interés sobre el capital invertido), como se muestra en la última columna de la tabla 7.7.
El gerente de producción desea la programación del número de motores que se deben fabricar en cada uno de los cuatro meses, de manera que se minimicen los costos totales de producción y almacenaje.
Una manera de formular un modelo matemático para este problema es definir xj como el número de motores de turbina que se producen en el mes j, para j =1,2,3,4. Con sólo estas cuatro variables de decisión, se puede formular el problema como un modelo de programación lineal que no se ajusta al tipo del problema de transporte.
El gerente de producción desea la programación del número de motores que se deben fabricar en cada uno de los cuatro meses, de manera que se minimicen los costos totales de producción y almacenaje.
Una manera de formular un modelo matemático para este problema es definir xj como el número de motores de turbina que se producen en el mes j, para j =1,2,3,4. Con sólo estas cuatro variables de decisión, se puede formular el problema como un modelo de programación lineal que no se ajusta al tipo del problema de transporte.
Etiquetas:
Problemas especiales de programación lineal
miércoles, 14 de mayo de 2014
Ejemplo de Programación de la Producción (I)
La Northern Airplane Company construye aviones comerciales para varias líneas aéreas en todo el mundo. La última etapa del proceso de producción consiste en fabricar los motores de turbina e instalarlos (operación sumamente rápido) en la estructura del avión terminado. La compañia tiene varios contratos de trabajo para entregar un gran número de aviones en un futuro cercano, y en este momento debe programarse la producción de los motores de turbina durante los próximos 4 meses.
En la segunda columna de la tabla 7.7 se indica la cantidad de motores que debe estar lista para su instalación, a fin de cumplir con las fechas de entrega contratadas. Así, el número acumulado en motores que deben producirse para fines de los meses 1,2,3 y 4 debe ser por lo menos 10, 25, 50 y 70, respectivamente.
Las instalaciones disponibles para producir los motores varían de acuerdo con otros programas de producción, mantenimiento y renovación durante este período. Las diferencias mensuales que resultan en cuanto al número máximo que se puede producir y e costo unitario de producción (en millones de dólares) se dan en la tercera y cuarta columnas de la tabla 7.7.
En la segunda columna de la tabla 7.7 se indica la cantidad de motores que debe estar lista para su instalación, a fin de cumplir con las fechas de entrega contratadas. Así, el número acumulado en motores que deben producirse para fines de los meses 1,2,3 y 4 debe ser por lo menos 10, 25, 50 y 70, respectivamente.
Las instalaciones disponibles para producir los motores varían de acuerdo con otros programas de producción, mantenimiento y renovación durante este período. Las diferencias mensuales que resultan en cuanto al número máximo que se puede producir y e costo unitario de producción (en millones de dólares) se dan en la tercera y cuarta columnas de la tabla 7.7.
Etiquetas:
Problemas especiales de programación lineal
martes, 13 de mayo de 2014
Propiedad de soluciones factibles
Una condición necesaria y suficiente para que un problema de transporte tenga soluciones factibles es que
Esta propiedad se puede verificar observando que las restricciones requieren que
Esta condición de que los recursos totales deben ser iguales a la demanda total exige en realidad que el sistema esté balanceado. Si el problema tiene algún significado físico y esta condición no se cumple, casi siempre significa que, o bien si, o bien dj de hecho representan una cota y no un requerimiento exacto. Si éste es el caso, se puede introducir un "origen" o "destino" imaginario (llamado origen ficticio o destino ficticio) para captar la holgura, con el fin de convertir las desigualdades en igualdades para satisfacer la condición de factibilidad. Los dos ejemplos que siguen explican cómo hacer esta conversión, y cómo ajustar otras variaciones comunes a la formulación del problema de transporte.
Esta propiedad se puede verificar observando que las restricciones requieren que
Etiquetas:
Problemas especiales de programación lineal
lunes, 12 de mayo de 2014
Propiedad de soluciones enteras
Para los problemas de transporte en los que si y dj tienen un valor entero, todas las variable básicas (asignaciones), en toda solución básica factible (incluyendo la óptima), tienen también valores enteros.
El procedimiento de solución que se describe en la sección 7.2 maneja sólo soluciones básicas factibles; entonces, en este caso obtendrá automáticamente, una solución óptima entera. Por tanto, no es necesario agregar al modelo de restricción de que xij debe tomar sólo valores enteros.
Sin embargo, para tener una solución óptima de cualquier tipo, un modelo de transporte debe tener soluciones factibles. La siguiente propiedad indica cuándo ocurre esto.
El procedimiento de solución que se describe en la sección 7.2 maneja sólo soluciones básicas factibles; entonces, en este caso obtendrá automáticamente, una solución óptima entera. Por tanto, no es necesario agregar al modelo de restricción de que xij debe tomar sólo valores enteros.
Sin embargo, para tener una solución óptima de cualquier tipo, un modelo de transporte debe tener soluciones factibles. La siguiente propiedad indica cuándo ocurre esto.
Etiquetas:
Problemas especiales de programación lineal
domingo, 11 de mayo de 2014
Modelo del problema de transporte (II)
Nótese que la tabla que resulta para los coeficientes de las restricciones tiene la estructura especial que se muestra en la tabla 7.6. Cualquier problema de programación lineal que se ajuste a esta formulación especial es del tipo de problemas de transporte, sin importar su contexto físico. De hecho, se han realizado numerosas aplicaciones no relacionadas con el transporte que se ajustan a esta estructura especial, como se verá en el siguiente ejemplo. (EL problema de asignación descrito en la sección 7.4 es un ejemplo adicional). Esta es una de las razones por las que el problema de transporte se suele considerar como uno de los tipos especiales de problemas de programación lineal más importantes.
En muchas aplicaciones, las cantidades de abastecimiento o recursos y de demanda (las si y dj) tienen valores enteros, al trabajar con el modelo se requerirá que las cantidades distribuidas (las xij) tomen también valores enteros. Por fortuna, gracias a la estructura especial que se muestra en la tabla 7.6,los problemas de este tipo tienen la siguiente propiedad.
En muchas aplicaciones, las cantidades de abastecimiento o recursos y de demanda (las si y dj) tienen valores enteros, al trabajar con el modelo se requerirá que las cantidades distribuidas (las xij) tomen también valores enteros. Por fortuna, gracias a la estructura especial que se muestra en la tabla 7.6,los problemas de este tipo tienen la siguiente propiedad.
Etiquetas:
Problemas especiales de programación lineal
sábado, 10 de mayo de 2014
Modelo del problema de transporte (I)
Para describir el modelo general del problema de transporte es necesario emplear términos que sean mucho menos específicos que los que se usaron para las componentes del ejemplo prototipo. En particular, el problema general de transporte se refiere (literal o figuradamente) a la distribución de cualquier bien desde cualquier grupo de centros de abastecimiento, llamados orígenes, a cualquier grupo de centros de recepción, llamados destinos, de tal manera que se minimicen los costos totales de distribución. La correspondencia en terminología entre el ejemplo prototipo y el problema general se resume en la tabla 7.4.
Así, por lo general, el destino i(i = 1,2,....,m) dispone de Si unidades para distribuir a los destinos y el destino j (j = 1,2,....,n) tiene una demanda de dj unidades que recibe desde los orígenes. Una suposición básica es que el costo de distribución de unidades desde el origen i al destino j es directamente proporcional al número distribuido, donde cij denota el costo por unidad distribuida. Igual que para el ejemplo prototipo, estos datos de entrada se pueden resumir en forma muy conveniente en la tabla de costos y requerimientos que se muestra en la tabla 7.5.
Sea Z el costo total de distribución y xij (i= 1,2,.....,m; j = 1,2,....,n) el número de unidades que distribuyen del origen i al destino j, la formulación de programación líneal para este problema es
Así, por lo general, el destino i(i = 1,2,....,m) dispone de Si unidades para distribuir a los destinos y el destino j (j = 1,2,....,n) tiene una demanda de dj unidades que recibe desde los orígenes. Una suposición básica es que el costo de distribución de unidades desde el origen i al destino j es directamente proporcional al número distribuido, donde cij denota el costo por unidad distribuida. Igual que para el ejemplo prototipo, estos datos de entrada se pueden resumir en forma muy conveniente en la tabla de costos y requerimientos que se muestra en la tabla 7.5.
Sea Z el costo total de distribución y xij (i= 1,2,.....,m; j = 1,2,....,n) el número de unidades que distribuyen del origen i al destino j, la formulación de programación líneal para este problema es
Etiquetas:
Problemas especiales de programación lineal
viernes, 9 de mayo de 2014
Problema del transporte - Ejemplo Prototipo (II)
Sujeta a las restricciones
La tabla 7.3 muestra los coeficientes de las restricciones. Como se verá en seguida, lo que distingue a este problema como un problema de transporte es la estructura especial en el patrón de estos coeficientes, no su contexto.
Entre paréntesis, la solución óptima para este problema es x11 = 0, x12 =20, x13 =0, x14 = 55, x21 = 80, x22=45, x23 = 0, x24 = 0, x31=0, x32 = 0, x33 = 70, x34 =30. Cuando se conozca la prueba de optimalidad que se explica en la sección 7.2, se podrá verificar este resultado (véase el problema 9).
La tabla 7.3 muestra los coeficientes de las restricciones. Como se verá en seguida, lo que distingue a este problema como un problema de transporte es la estructura especial en el patrón de estos coeficientes, no su contexto.
Entre paréntesis, la solución óptima para este problema es x11 = 0, x12 =20, x13 =0, x14 = 55, x21 = 80, x22=45, x23 = 0, x24 = 0, x31=0, x32 = 0, x33 = 70, x34 =30. Cuando se conozca la prueba de optimalidad que se explica en la sección 7.2, se podrá verificar este resultado (véase el problema 9).
Etiquetas:
Problemas especiales de programación lineal
jueves, 8 de mayo de 2014
Problema del transporte - Ejemplo Prototipo (I)
Uno de los productos más importantes de la P&T Company son el chícharo enlatado. Los chícharos se preparan en tres enlatadoras (cercanas a Bellingham, Washington; a Eugene, Oregon, y Albert Lea, Minnesota) y después se mandan por camión a cuatro almacenes de distribución (Sacramento, California; Salta Lake City, Utah; Rapid City, South Dakota y Alburquerque, Nuevo Mexico) en el oeste de EStados Unidos, como se muestra en la figura 7.1. Debido a que los costos de embarque constituyen un gasto importante, la gerencia ha iniciado un estudio para reducirlos lo más que se pueda. Se ha hecho una estimación de la producción de cada enlatadora para la próxima temporada y se ha asignado a cada almacén una cierta cantidad de la producción total de chícharos. En la tabla 7.2 se proporciona esta información (en unidades de carga de camión), junto con el costo de transporte por camón cargado para cada combinación de enlatadora-almacén. Como se ve, hay un total de 300 cargas de camión que se deben transportar. El problema es determinar el plan de asignación de estos embarques a las distintas combinaciones de enlatadora-almacén que minimice el costo total de transporte.
Éste, de hecho, es un problema de programación lineal del tipo de los problemas de transporte. Para formularlo, sea Z el costo total de transporte y sea xij (i = 1,2,3; j = 1,2,3,4) el número de cargas de camión que se mandan de la enlatadora i al almacén j. Entonces el objetivo es seleccionar los valores de estas 12 variables de decisión (las xij) para
Minimizar Z = 464x11 + 513x12 + 654x13 + 867x14 + 352x21 + 416x22
+690x23 + 791x24 + 995x31 + 682x32 + 388x33 + 685x34
Éste, de hecho, es un problema de programación lineal del tipo de los problemas de transporte. Para formularlo, sea Z el costo total de transporte y sea xij (i = 1,2,3; j = 1,2,3,4) el número de cargas de camión que se mandan de la enlatadora i al almacén j. Entonces el objetivo es seleccionar los valores de estas 12 variables de decisión (las xij) para
Minimizar Z = 464x11 + 513x12 + 654x13 + 867x14 + 352x21 + 416x22
+690x23 + 791x24 + 995x31 + 682x32 + 388x33 + 685x34
Etiquetas:
Problemas especiales de programación lineal
miércoles, 7 de mayo de 2014
Problemas especiales de programación lineal (II)
Tal vez el tipo especial más importante de problemas de programación lineal sea el llamado problema de transporte, y se describirá en primer lugar. También se presentará en parte su procedimiento de solución para ilustrar la simplificación del método símplex que puede obtenerse al explotar la estructura especial del problema. Después se expondrán otros dos problemas especiales de programación lineal (el problema de transbordo y el problema de la asignación) que tienen una estrecha relación con el problema del transporte; por último, se describirá un tipo especial de problemas que surgen con frecuencia en las organizaciones multidivisionales.
Etiquetas:
Problemas especiales de programación lineal
martes, 6 de mayo de 2014
Problemas especiales de programación lineal (I)
En el capítulo 3 se hizo hincapié en una amplia variedad de aplicaciones de programación líneal. En este capítulo se seguirá ampliando el horizonte al presentar algunos tipos particularmente importantes de problemas de programación líneal. Estos tipos especiales comparten varias características centrales. La primera es que todos surgen con frecuencia en diferentes contextos de la vida real. También tienden a requerir un número muy grande de variables y restricciones, por lo que la aplicación directa del método símplex en una computadora puede significar un esfuerzo computacional exorbitante. Por fortuna, otra carecterística es que la mayor parte de los coeficientes aij en las restricciones son ceros, y aquellos que son distintos de cero siguen un patrón preciso . Como resultado de estas características, ha sido posible desarrollar versiones simplificadas del método símplex que logran enromes ahorros computacionales al explotar la estructura especial del problema. Por lo tanto, es importante famializarse con estos problemas especiales para que se reconozcan cuando surjan y se pueda aplicar el procedimiento computacional adecuado.
Para describir las estructuras especiales se introducirá la tabla (o matriz) de coeficientes que se muestra en la tabla 7.1, en donde aij es el coeficiente de la j-ésima variable en la i-ésima restricción funcional. Más adelante, las partes de la tabla que contienen coeficientes iguales a cero se indicarán dejándolas en blanco, mientras que los bloques en donde hay coeficientes distintos de cero se indicarán con áreas sombreadas.
Para describir las estructuras especiales se introducirá la tabla (o matriz) de coeficientes que se muestra en la tabla 7.1, en donde aij es el coeficiente de la j-ésima variable en la i-ésima restricción funcional. Más adelante, las partes de la tabla que contienen coeficientes iguales a cero se indicarán dejándolas en blanco, mientras que los bloques en donde hay coeficientes distintos de cero se indicarán con áreas sombreadas.
Etiquetas:
Problemas especiales de programación lineal
lunes, 5 de mayo de 2014
Conclusiones Teoría de dualidad y análisis de sensibilidad
Todo problema de programación lineal tiene, asociado a él, un problema de programación lineal dual. Existen ciertas relaciones útiles entre el problema original (primal) y su problema dual que refuerzan la habilidad para analizar el problema primal. Por ejemplo, la interpretación económica del problema dual proporciona los precios sombra que miden el valor marginal de los recursos en el problema primal, al igual que permiten dar una interpretación del método símplex. Puesto que el método símplex se puede aplicar directamente a cualquiera de los dos problemas para obtener la solución de ambos al mismo tiempo, es posible ahorrar una gran cantidad de esfuerzo computacional si se maneja directamente el problema dual. La teoría de dualidad, que incluye el método símplex dual para trabajar con soluciones básicas superóptimas, juega un papel de gran importancia en el análisis de sensibilidad.
Los valores usados como parámetros de un modelo de programación lineal son sólo estimaciones. Por lo tanto, es necesario llevar a cabo el análisis de sensibilidad para investigar lo que ocurre si las estimaciones están equivocadas. La idea fundamental de la sección 5.3 proporciona la clave para realizar esta investigación de manera eficiente. Los objetivos generales son identificar los parámetros relativamente sensibles que afectan la solución óptima, para tratar de estimarlos con más cuidado y después elegir una solución que se mantenga como buena en un cierto intervalo de valores posibles de estos parámetros sensibles. Este análisis constituye una parte muy importante de los estudios de programación líneal.
domingo, 4 de mayo de 2014
Análisis de sensbilidad sistemático - Programación paramétrica (IX)
Como ya se dijo en la sección 4.7, esta manera de variar en forma continua varios parámetros al mismo tiempo se conoce con el nombre de programación lineal paramétrica. En la sección 9.3 se presenta el procedimiento completo (incluyendo la identificación de nuevas soluciones óptimas para valores más grandes de θ) Cuando sólo se varían los parámetros cj y después cuando sólo varían los parámetros de una sola restricción. Además de las aplicaciones que se mencionaron en la sección 4.7, este procedimiento proporciona una forma conveniente de llevar a cabo un análisis de sensibilidad sistemático.
sábado, 3 de mayo de 2014
Análisis de sensbilidad sistemático - Programación paramétrica (VIII)
El procedimiento algebraico para manejar estos dos cambios, Δc1 = θ y Δc2 = -2θ simultáneamente, es parecido al que se muestra en la tabla 6.22 (para Δc2 = ±1 para otra versión del modelo). Aunque los cambios ahora se expresan en términos de θ en lugar de se cantidades númericas específicas, θ se maneja justo como un número desconocido. La tabla 6.24 muestra los resultados de este procedimiento, incluyendo sólo los renglones relevantes de la tabla símplex en cuestión (el renglón 0 y el renglón para la variable básica x2). La primera tabla símplex que se muestra es justo la tabla símplex final para la versión actual del modelo (antes de cambiar c1 y c2) según la tabla 6.20. Usando las fórmulas de la tabla 6.17, el único cambio en la tabla símplex final revisada que se muestra en la segunda es que Δc1 y Δc2 se restan de los coficientes de x1 y x2, respectivamente. Para convertir esta tabla símplex a la forma apropiada de eliminación de Gauss se resta del renglón 0 el renglón 2 multiplicado por 2θ, lo que lleva a la última tabla símplex que se muestra. Las expresiones en términos de θ para los coeficientes de las variables no básicas (x1 y x5) en el renglón 0 de esta tabla indican que la solución básica factible actual sigue siendo óptima para θ ≤ 9/8. Como θ = 1 es el máximo valor realista de θ, se puede decir que c1 y c2 juntos son parámetros no sensibles respecto al modelo de ta tabla 6.20. No hay necesidad de tratar de estimar el valor de estos parámetros a menos que otros parámetros cambien (como ocurre en el ejemplo del caso 3).
viernes, 2 de mayo de 2014
Análisis de sensbilidad sistemático - Programación paramétrica (VII)
En particular, es apropiado considerar estos cambios simultáneos si existen factores que causan que los parámetros cambien al mismo tiempo. Son compentitivos los productos de algún sentido, de forma que una ganancias unitaria más grande que la esperada para uno implica una ganancias por unidad menor que la esperada para el otro? EStán los os productos afectados por algún factor externo como una campaña publicitaria de un competidor? Es posible cambiar ambas ganancias unitarias a través de cambios apropiados de personal y equipo?
Haciendo referencia a la región factible de la figura 6.3, la interpretación geométrica de cambiar la función objetivo de Z = 3x1 + 5x2 a Z(θ) = (3 + θ)x1 + (5 - 2θ)x2 es que se cambia la pendiente de la recta de la función objetivo original Z = 45 = 3x1 + 5x2, que pasa por la solución óptima (0,9). Si el valor de θ se aumenta lo suficiente, esta pendiente cambiará hasta que la solución óptima se traslade de (0,9) a otra solución factible en un vértice (4, 3). (verífiquese en la gráfica si esto ocurre para θ ≤ 1.)
jueves, 1 de mayo de 2014
Análisis de sensbilidad sistemático - Programación paramétrica (VI)
El enfoque para cambiar varios parámetros cj al mismo tiempo es similar. En este caso, se expresa en el nuevo valor de cj en términos del valor original de cj como sigue
cj = cj + αj θ, para = j =1,2,....., n
en donde las αj son constantes de entrada que especifican la tasa deseada de incremento (positiva o negativa) de cj al aumentar el valor de θ.
Para ilustrar este caso, reconsidérese el análisis de sensibilidad de c1 y c2 para el problema de la Wyndor Glass Co, que se realizo antes en esta sección. Comenzando con la versión del modelo que se presenta en la tabla 6.20 y la figura 6.3, se estudiará por separado el efecto de cambiar c1 de 3 a 4 (su estimación más optimista) y c2 de 5 a 3 (su estimación más pesimista). Ahora se pueden considerar simultáneamente ambos cambios, al igual que varios casos intermedios con cambios más pequeños, estableciendo.
c1 = 3 + θ, c2 = 5 - 2θ
en donde el valor de θ mide la fracción del máximo cambio posible que se hace. El resultado es reemplazar la función objetivo orginal, Z = 3x1 + 5x2, por una función de θ,
Z(θ) = (3 + θ)x1 + (5 - 2θ)x2,
de forma que ahora se puede realizar la optimización para cualquier valor deseado (fijo) de θ entre 0 y 1. Al verificar el efecto de que θ aumente de 0 a 1, se puede determinar con exactitud cuándo y cómo cambia la solución óptima al aumentar el error en las estimaciones de estos parámetros originales.
Suscribirse a:
Entradas (Atom)