Cuando se aplica el método símplex a formas primales no estándar y cuando se usa la técnica de variables artificiales (quizá con la ayuda del método de la M) para adaptarse a ellas, también debe hacerse algún ajuste a la interpretación de dualidad del renglón 0. Esto se debe a que las variables artificiales y las cantidades M revisan el problema primal y, por lo tanto, el problema dual cambia y las soluciones básicas complementarias que se muestran en el renglón 0 son soluciones de este problema dual revisado. Sin embargo, una vez que se han elminado las variables artificiales (se han hecho no básicas) y que la solución actual es una solución básica factible legítima para el problema primal original, se puede usar el renglón 0 para identificar la solución básica complementaria para el problema dual original. En seguida se describirá cómo se hace esto.
Supóngase que se usa la forma de la primera columna de la tabla 6.14. Para cada restricción de igualdad i, su variable artificial juega el papel de variable de holgura, excepto que al principio se agrego M al coeficiente de esta variable en el renglón 0. Por tanto, el valor actual de al variable dual correspondiente yi, es el coeficiente actual de esta variable artificial menos M. Su una restricción del tipo ≤ tiene lado derecho negativo desde el inicio (tal vez era una restricción ≥ y se cambió), de manera que se le ha agregado una variable artificial, el valor de la variable dual correspondiente sigue siendo el coeficiente de su variable de holgura. En este caso se ignora el coeficiente de la variable artificial. Por último, si la variable x es no restringirla en signo y se ha sustituido por la diferencia de dos variables no negativas (xj^+ - xj^-), el coeficiente de xj^+, denotado por (zj^+ - cj), se usará como si se tratara de xj. En otras palabras,

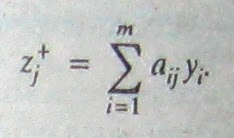
No hay comentarios.:
Publicar un comentario