Preparación para el método símplex (V)

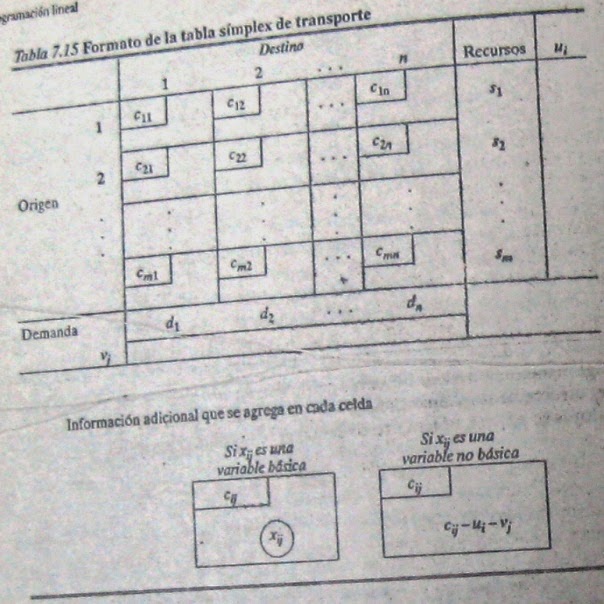
La gran conclusión es que se puede eliminar casi toda la tabla símplex (junto con todo el esfuerzo de actualizarla)! Además de los datos de entrada (los valores de cij, si y dj), la única información que necesita el método símplex de transporte es la solución básica factible actual, los valores actuales de ui y vj y los valores resultantes de (cij -ui - vj) para las variables xij no básicas. Cuando se resuelve un problema a mano es conveniente registrar esa información en una tabla símplex de transporte, como la que se muestra en la tabla 7.15. [Obsérvese con cuidado que los valores de xij y (cij - ui -vj) se distinguen en esta tabla encerrando en un círculo los primeros pero no estos últimos].

El lector podrá apreciar de manera global la gran diferencia en eficiencia y conveniencia entre los métodos símplex de transporte y símplex si aplica ambos al mismo problema pequeño (véase el problema 22). Sin embargo, la diferencia es más importante en problemas grandes que tienen que resolverse en una computadora. El tamaño de las tablas símplex y de transporte sugiere, de alguna manera, esta gran ganancia. Para un problema de transporte que tiene m orígenes y n destinos, la tabla símplex tiene (m+n+1) renglones  y (m+1)(n+1) columnas (sin incluir las que se colocan a la izquierda de las columnas de xij), y la  tabla símplex de transporte tendrá m renglones y n columnas (excluyendo los dos renglones y columnas de información adicional). Si se dan valores a m y n (por ejemplo, m = 10 y n =100, que sería un problema bastante normal de tamaño mediano), se puede observar cómo crece la razón del número de celdas en la tabla símplex entre el mismo número en la tabla de transporte, conforme m y n crecen.